2022-2023學(xué)年福建省寧德十二中八年級（上）第三次月考數(shù)學(xué)試卷

一．選擇題

• 1．下列運(yùn)算正確的是（　　）

  A．a(chǎn)3?a4=a12

  B．（a3）3=a6

  C．a(chǎn)4÷a3=a

  D．a(chǎn)3+a4=a7
  組卷：56引用：5難度：0.6

  解析

• 2．計(jì)算（a²b）³的結(jié)果是（　　）

  A．a(chǎn)2b3

  B．3a2b

  C．a(chǎn)6b3

  D．a(chǎn)8b3
  組卷：75引用：5難度：0.9

  解析

• 3．計(jì)算2²⁰¹⁹×（-

  1

  2

  ）²⁰²⁰的值是（　　）

  A．-1

  B． 1 2

  C．- 1 2

  D．1
  組卷：1992引用：4難度：0.7

  解析

• 4．下列各式中與a-b-c的值相等的是（　　）

  A．a(chǎn)-（b-c）	B．a(chǎn)+（b-c）
  C．（a-b）-（-c）=a-b+c	D．（a-b）+（-c）
  組卷：14引用：1難度：0.7

  解析

• 5．設(shè)a^m=2，aⁿ=6，則a^2m+n=（　　）

  A．18

  B．20

  C．22

  D．24
  組卷：12引用：3難度：0.6

  解析

• 6．（5a-4b）（____）=25a²-16b²括號內(nèi)應(yīng)填（　　）

  A．5a-4b

  B．5a+4b

  C．-5a+4b

  D．-5a-4b
  組卷：30引用：3難度：0.6

  解析

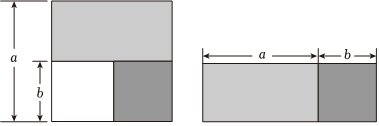• 7．如圖，從邊長為a的正方形中去掉一個(gè)邊長為b的小正方形，然后將剩余部分剪后拼成一個(gè)長方形，上述操作能驗(yàn)證的等式是（　　）

  A．（a+b）（a-b）=a2-b2	B．（a-b）2=a2-2ab+b2
  C．（a+b）2=a2+2ab+b2	D．a(chǎn)2+ab=a（a+b）
  組卷：3976引用：42難度：0.9

  解析

三．解答題

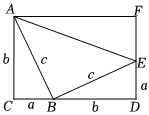• 22．如圖，在長方形ACDF中，AC=DF，點(diǎn)B在CD上，點(diǎn)E在DF上，BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE．
  （1）用兩種不同的方法表示出長方形ACDF的面積S，并探求a,b,c之間的等量關(guān)系（需要化簡）
  （2）請運(yùn)用（1）中得到的結(jié)論，解決下列問題：
  ①求當(dāng)c=5，a=3時(shí)，求S的值；
  ②當(dāng)c-b=8，a=12時(shí)，求S的值．
  組卷：337引用：4難度：0.5

  解析

• 23．教科書中這樣寫道：“我們把多項(xiàng)式a²+2ab+b²及a²-2ab+b²叫做完全平方式”，如果一個(gè)多項(xiàng)式不是完全平方式，我們常做如下變形：先添加一個(gè)適當(dāng)?shù)捻?xiàng)，使式子中出現(xiàn)完全平方式，再減去這個(gè)項(xiàng)，使整個(gè)式子的值不變，這種方法叫做配方法．配方法是一種重要的解決問題的數(shù)學(xué)方法，不僅可以將一個(gè)看似不能分解的多項(xiàng)式分解因式，還能解決一些與非負(fù)數(shù)有關(guān)的問題或求代數(shù)式最大值，最小值等．
  例如：分解因式x²+2x-3=（x²+2x+1）-4=（x+1）²-4=（x+1+2）（x+1-2）=（x+3）（x-1）；例如求代數(shù)式2x²+4x-6的最小值.2x²+4x-6=2（x²+2x-3）=2（x+1）²-8．可知當(dāng)x=-1時(shí)，2x²+4x-6有最小值，最小值是-8，根據(jù)閱讀材料用配方法解決下列問題：
  （1）分解因式：m²-4m-5=

  ．
  （2）當(dāng)a,b為何值時(shí)，多項(xiàng)式a²+b²-4a+6b+18有最小值，并求出這個(gè)最小值．
  （3）當(dāng)a,b為何值時(shí)，多項(xiàng)式a²-2ab+2b²-2a-4b+27有最小值，并求出這個(gè)最小值．
  組卷：4089引用：9難度：0.1

  解析