2022-2023學(xué)年廣東省廣州市華南師大附中高一（上）期末數(shù)學(xué)試卷

一、單選題：本大題共8小題，每小題3分，滿分24分.在每小題給出的四個選項中，只有一項符合題目要求.

• 1．已知集合

  A

  =

  {

  x

  |

  1

  9

  ≤

  3

  x

  ＜

  9

  }

  ，集合B={x|log₃x＜1}，則A∩B=（　　）

  A．（0，2）

  B．[-2，3）

  C．[0，2）

  D．[-2，0）
  組卷：243引用：8難度：0.8

  解析

• 2．“sinθ=1”是“

  θ

  =

  π

  2

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：175引用：5難度：0.7

  解析

• 3．命題“?x＞0，x²+x+1≥0”的否定是（　　）

  A．?x≤0，x2+x+1＜0	B．?x＞0，x2+x+1＜0
  C．?x≤0，x2+x+1≥0	D．?x＞0，x2+x+1＜0
  組卷：264引用：10難度：0.8

  解析

• 4．不等式

  2

  x

  +

  3

  x

  -

  1

  ≥

  1

  的解集為（　　）

  A． { x | x ＜ 1 或 x ≥ 3 2 }

  B．{x|x≥4}

  C．{x|x≤-4}

  D．{x|x＞1或x≤-4}
  組卷：149引用：2難度：0.8

  解析

• 5．已知二次函數(shù)y=x²-2ax+1在區(qū)間（2，3）內(nèi)是單調(diào)函數(shù)，則實數(shù)a的取值范圍是（　　）

  A．（-∞，2]∪[3，+∞）	B．[2，3]
  C．（-∞，-3]∪[-2，+∞）	D．[-3，-2]
  組卷：243引用：4難度：0.8

  解析

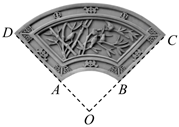• 6．磚雕是我國古建筑雕刻中的重要藝術(shù)形式，傳統(tǒng)磚雕精致細(xì)膩、氣韻生動、極富書卷氣．如圖所示，一扇環(huán)形磚雕，可視為將扇形OCD截去同心扇形OAB所得圖形，已知OA=0.2m,AD=0.3m,∠AOB=100°，則該扇環(huán)形磚雕的面積為（　　）m²．

  A． π 6

  B． π 12

  C． π 18

  D． 7 π 120
  組卷：253引用：9難度：0.7

  解析

• 7．已知角α的終邊過點（-1，2），則

  sin

  （

  3

  π

  -

  α

  ）

  -

  cos

  （

  π

  2

  +

  α

  ）

  +

  sin

  （

  11

  π

  2

  +

  α

  ）

  的值為（　　）

  A． 5 5

  B． 2 5 5

  C． 4 5 5

  D． 5
  組卷：667引用：4難度：0.7

  解析

四、解答題：本大題共6小題，滿分52分.解答應(yīng)寫出文字說明、證明過程或演算過程.

• 21．已知函數(shù)

  f

  （

  x

  ）

  =

  1

  2

  （

  si

  n

  4

  x

  -

  co

  s

  4

  x

  ）

  +

  3

  sinxcosx

  ．
  （1）求函數(shù)f（x）的最小正周期；
  （2）令

  g

  （

  x

  ）

  =

  f

  2

  （

  x

  ）

  +

  af

  （

  x

  ）

  +

  3

  -

  a

  ,

  x

  ∈

  [

  π

  12

  ，

  5

  π

  12

  ]

  ，求g（x）的最小值．
  組卷：280引用：1難度：0.5

  解析

• 22．給定常數(shù)a＞0，定義在R上的函數(shù)

  f

  （

  x

  ）

  =

  1

  2

  sin

  （

  5

  π

  2

  -

  2

  x

  ）

  +

  asinx

  ．
  （1）若f（x）在R上的最大值為2，求a的值；
  （2）設(shè)

  a

  ≥

  1

  2

  ，

  n

  為正整數(shù)．如果函數(shù)y=f（x）在區(qū)間（0，nπ）內(nèi)恰有2022個零點，求n的值．
  組卷：182引用：2難度：0.5

  解析