2022-2023學(xué)年廣東省深圳市龍崗區(qū)百合外國(guó)語學(xué)校九年級(jí)（下）期中數(shù)學(xué)試卷

一、選擇題：（本題10個(gè)小題，每題3分，共30分

• 1．下列說法中，正確的是（　　）

  A．3與-3互為倒數(shù)	B．3與 1 3 互為相反數(shù)
  C．0的相反數(shù)是0	D．5的絕對(duì)值是-5
  組卷：191引用：6難度：0.8

  解析

• 2．貼窗花是我國(guó)春節(jié)喜慶活動(dòng)的一個(gè)重要內(nèi)容，它起源于西漢時(shí)期，歷史悠久，風(fēng)格獨(dú)特，深受國(guó)內(nèi)外人士的喜愛．下列窗花作品為軸對(duì)稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：278引用：9難度：0.9

  解析

• 3．《百合綻放》是百合外國(guó)語學(xué)校在20年校慶之際，融入全校教職工和學(xué)生智慧于一體而編寫的，該書凸顯了百外建校以來的“和合而生”的教育理念和收括了許多的教育案例，該書第一次印刷就出版了5500冊(cè)．將5500用科學(xué)記數(shù)法表示為（　　）

  A．0.55×104

  B．5.5×103

  C．5.5×104

  D．55×102
  組卷：25引用：1難度：0.7

  解析

• 4．下列運(yùn)算正確的是（　　）

  A．a(chǎn)6÷a2=a3	B．a(chǎn)2+a3=a5
  C．-2（a+b）=-2a+b	D．（-2a2）2=4a4
  組卷：207引用：4難度：0.7

  解析

• 5．費(fèi)爾茲獎(jiǎng)是國(guó)際上享有崇高聲譽(yù)的一個(gè)數(shù)學(xué)獎(jiǎng)項(xiàng)，每四年評(píng)選一次，主要授予年輕的數(shù)學(xué)家．下面數(shù)據(jù)是部分獲獎(jiǎng)?wù)攉@獎(jiǎng)時(shí)的年齡（單位：歲）：31，32，33，35，35，39，則這組數(shù)據(jù)的眾數(shù)和中位數(shù)分別是（　　）

  A．35，35

  B．34，33

  C．34，35

  D．35，34
  組卷：153引用：5難度：0.6

  解析

• 6．一個(gè)布袋中放著6個(gè)黑球和18個(gè)紅球，除了顏色以外沒有任何其他區(qū)別．則從布袋中任取1個(gè)球，取出黑球的概率是（　　）

  A． 1 4

  B． 1 3

  C． 2 3

  D． 3 4
  組卷：377引用：3難度：0.8

  解析

• 7．如圖所示，直線a∥b,直線c分別交a,b于點(diǎn)A，C，點(diǎn)B在直線b上AB⊥AC，若∠1=140°，則∠2的度數(shù)是（　　）

  A．30°

  B．40°

  C．50°

  D．70°
  組卷：273引用：2難度：0.7

  解析

三、解答題：（本題7個(gè)小題，共55分）

• 21．《幾何原本》是古希臘數(shù)學(xué)家歐幾里得的一部不朽著作，是數(shù)學(xué)發(fā)展史的一個(gè)里程碑．在該書的第2卷“幾何與代數(shù)”部分，記載了很多利用幾何圖形來論證的代數(shù)結(jié)論，利用幾何給人以強(qiáng)烈印象將抽象的邏輯規(guī)律體現(xiàn)在具體的圖形之中．
  （1）我們?cè)趯W(xué)習(xí)許多代數(shù)公式時(shí)，可以用幾何圖形來推理，觀察下列圖形，找出可以推出的代數(shù)公式，（下面各圖形均滿足推導(dǎo)各公式的條件，只需填寫對(duì)應(yīng)公式的序號(hào)）
  
  公式①：（a+b+c）d=ad+bd+cd
  公式②：（a+b）（c+d）=ac+ad+bc+bd
  公式③：（a-b）²=a²-2ab+b²
  公式④：（a+b）²=a²+2ab+b²
  圖1對(duì)應(yīng)公式

  ，圖2對(duì)應(yīng)公式

  ，圖3對(duì)應(yīng)公式

  ，圖4對(duì)應(yīng)公式

  ．
  （2）《幾何原本》中記載了一種利用幾何圖形證明平方差公式（a+b）（a-b）=a²-b²的方法，如圖5，請(qǐng)寫出證明過程；（已知圖中各四邊形均為矩形）
  （3）如圖6，在等腰直角三角形ABC中，∠BAC=90°，D為BC的中點(diǎn)，E為邊AC上任意一點(diǎn)（不與端點(diǎn)重合），過點(diǎn)E作EG⊥BC于點(diǎn)G，作EH⊥AD于點(diǎn)H，過點(diǎn)B作BF∥AC交EG的延長(zhǎng)線于點(diǎn)F．記△BFG與△CEG的面積之和為S₁，△ABD與△AEH的面積之和為S₂．
  ①若E為邊AC的中點(diǎn)，則

  S

  1

  S

  2

  的值為

  ；
  ②若E不為邊AC的中點(diǎn)時(shí)，試問①中的結(jié)論是否仍成立？若成立，寫出證明過程；若不成立，請(qǐng)說明理由．
  
  組卷：940引用：4難度：0.1

  解析

• 22．閱讀材料：小百合特別喜歡探究數(shù)學(xué)問題，一天萬老師給她這樣一個(gè)幾何問題：
  如圖1，△ABC和△BDE都是等邊三角形，將△BDE繞著點(diǎn)B旋轉(zhuǎn)α°，求證：AE=CD．
  【探究發(fā)現(xiàn)】（1）小百合很快就通過△ABE≌△CBD，論證了AE=CD，于是她想，把等邊△ABC和等邊△BDE都換成等腰直角三角形，如圖2，將△BDE繞著點(diǎn)B旋轉(zhuǎn)α°，其中∠ACB=∠EDB=90°那么AE和CD有什么數(shù)量關(guān)系呢？請(qǐng)寫出你的結(jié)論，并給出證明．
  【拓展遷移】（2）如果把等腰直角三角形換成正方形，如圖3，將正方形AFEG繞點(diǎn)A旋轉(zhuǎn)α°，若AB=6

  2

  ，AG=4，在旋轉(zhuǎn)過程中，當(dāng)C，G，E三點(diǎn)共線時(shí)，請(qǐng)直接寫出DG的長(zhǎng)度．
  【拓展延伸】（3）小百合繼續(xù)探究，做了如下變式：如圖4，矩形ABCD≌矩形FECG，且具有公共頂點(diǎn)C，將矩形ABCD固定，另一個(gè)矩形FECG繞著點(diǎn)C順時(shí)針旋轉(zhuǎn)α°（0＜α＜90），連接AF、DG，直線GD交AF于點(diǎn)H，在旋轉(zhuǎn)的過程中，試證明H為AF的中點(diǎn)．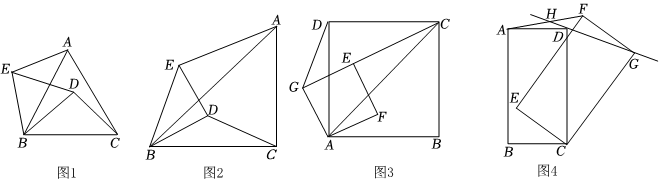
  
  組卷：308引用：1難度：0.4

  解析