當前位置：試卷中心 > 試卷詳情

2023-2024學年重慶市北碚區西南大學附中九年級（上）開學數學試卷

發布：2024/7/28 8:0:9

一.選擇題（共10小題，滿分40分，每小題4分）

1．下列各圖是選自歷屆世界大運會的會徽圖案，其中是軸對稱圖形的是（　　）
A． B． C． D．
組卷：82引用：2難度：0.9
解析
2．如圖，△ABC與△DEF位似，點O為位似中心．已知OA：OD=1：3，且△ABC的周長為4，則△DEF的周長為（　　）
A．8 B．12 C．16 D．36
組卷：152引用：4難度：0.7
解析
3．對于二次函數y=3（x+4）²，其圖象的頂點坐標為（　　）
A．（0，4） B．（0，-4） C．（4，0） D．（-4，0）
組卷：86引用：10難度：0.6
解析
4．估計
32
-
4
÷2的運算結果在哪兩個整數之間（　　）
A．3和4 B．4和5 C．5和6 D．6和7
組卷：137引用：3難度：0.7
解析
5．如圖，是由一些小棒搭成的圖案，按照這種方式擺下去，擺第9個圖案所用小棒的數量為（　　）
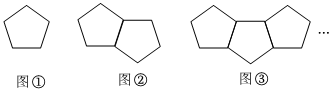
A．33 B．36 C．37 D．41
組卷：303引用：8難度：0.6
解析
6．我市某家快遞公司，今年8月份與10月份完成投遞的快遞總件數分別為2萬件和2.88萬件．若設該快遞公司由8月份到10月份投遞總件數的月平均增長率為x,則以下所列方程正確的是（　　）
A．2（1+x）=2.88
B．2（1+2x）=2.88
C．2（1+x）²=2.88
D．2+2（1+x）+2（1+x）²=2.88
組卷：299引用：4難度：0.5
解析
7．如圖，在△ABC中，∠ABC=60°，∠C=45°，AD⊥BC，垂足為D，∠ABC的平分線交AD于點E，若
AE
=
6
，則AC的長為（　　）
A．
2
3
B．
3
3
2
C．
3
3
D．
3
6
2
組卷：77引用：3難度：0.5
解析
8．二次函數y=ax²+bx+c（a≠0）的圖象的一部分如圖所示．已知圖象經過點（-1，0），其對稱軸為直線x=1．下列結論：①abc＜0；②8a+c＜0；③a+b≥am²+bm；④不等式ax²+bx+c＞0的解集是-1＜x＜3；⑤若拋物線經過點（-3，n），則關于x的一元二次方程ax²+bx+c-n=0（a≠0）的兩根分別為x₁=4、x₁=-3．上述結論中正確結論的個數為（　　）
A．1個 B．2個 C．3個 D．4個
組卷：613引用：5難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三.解答題（共8小題，滿分78分）

25．如圖，在平面直角坐標系中，拋物線
y
=
2
3
x
2
+
4
3
x
-
2
與x軸交于A，B兩點（點A在點B的左側），與y軸交于點C．
（1）求線段AC的長度；
（2）點P為直線AC下方拋物線上的一動點，且點P在拋物線對稱軸左側，過點P作PD∥y軸，交AC于點D，作PE∥x軸，交拋物線于點E．求3PD+PE的最大值及此時點P的坐標；
（3）在（2）中3PD+PE取得最大值的條件下，將該拋物線沿著射線CA方向平移
13
個單位長度，得到一條新拋物線y′，M為射線CA上的動點，過點M作MF∥x軸交新拋物線y′的對稱軸于點F，點N為直角坐標系內一點，請直接寫出所有使得以點P，F，M，N為頂點的四邊形是菱形的點N的坐標，并寫出求解點N的坐標的其中一種情況的過程．
?
組卷：810引用：5難度：0.1
解析
26．在△ABC中，90°＜∠BAC＜120°，將線段AB繞點A逆時針旋轉120°得到線段AD，連接CD．
（1）如圖1，若AB=8，∠ABC=45°，BA⊥CD，延長BA，CD交于點K，求四邊形ABCD的面積；
（2）如圖2，點E是CA延長線上一點，點G是AE的中點，連接BE，BG，點F在線段AC上，點H在線段BG上，連接HF，若BG=GF，HF=BE，GA=GH，2∠ACB=∠EBG+∠ABC，求證：BC+CD=
3
AC；
（3）如圖3，在（1）的條件下，點P是線段BC上的一個動點，連接DP，將線段DP繞點D逆時針旋轉45°得到線段DP'，連接AP'，BP'，點M是△ABP'內任意一點，點P在運動過程中，AM+BM+P'M是否存在最小值；若存在，請直接寫出：AM+BM+P'M的最小值；若不存在，請說明理由．
組卷：664引用：3難度：0.1
解析