2022-2023學年河南省南陽三中九年級（上）期末數學試卷

一、選擇題（30分）

• 1．下列各式是最簡二次根式的是（　　）

  A． 9

  B． 25 2

  C． 50

  D． x 4 + y 4
  組卷：877引用：3難度：0.8

  解析

• 2．方程x（x-6）=x的根是（　　）

  A．x=6

  B．x1=0，x2=-7

  C．x1=0，x2=7

  D．x1=0，x2=6
  組卷：476引用：4難度：0.6

  解析

• 3．已知（-3，y₁），（-2，y₂），（1，y₃）是拋物線y=-3x²-12x+m上的點，則（　　）

  A．y3＜y2＜y1

  B．y3＜y1＜y2

  C．y2＜y3＜y1

  D．y1＜y3＜y2
  組卷：6421引用：45難度：0.5

  解析

• 4．用※定義一種新運算：對于任意實數m和n,規定m※n=m²n-mn-3n,如：1※2=1²×2-1×2-3×2=-6．則（-2）※

  3

  結果為（　　）

  A． 3 3

  B． - 2 3

  C． 3 2

  D． 2 3
  組卷：2080引用：16難度：0.7

  解析

• 5．二次函數y=ax²+bx+c（a≠0）的圖象是拋物線G，自變量x與函數y的部分對應值如下表：
  

  x	…	-5	-4	-3	-2	-1	0	…
  y	…	4	0	-2	-2	0	4	…

  下列說法正確的是（　　）

  A．拋物線G的開口向下

  B．拋物線G的對稱軸是直線x=-2

  C．拋物線G與y軸的交點坐標為（0，4）

  D．當x＞-3時，y隨x的增大而增大
  組卷：1255引用：16難度：0.6

  解析

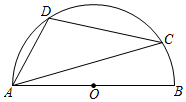• 6．如圖，AB是半圓的直徑，C、D是半圓上的兩點，∠ADC=106°，則∠CAB等于（　　）

  A．10°

  B．14°

  C．16°

  D．26°
  組卷：3537引用：23難度：0.8

  解析

• 7．⊙O的半徑為10cm,弦AB∥CD，AB=16cm,CD=12cm,則AB，CD間的距離是（　　）

  A．2cm

  B．14cm

  C．2cm或14cm

  D．6cm或8cm
  組卷：187引用：3難度：0.5

  解析

三、解答題（75分）

• 22．如圖1，在矩形ABCD中，AB=10，BC=12，點M是BC邊上的動點，點M從點B出發，運動到點C停止，N是CD邊上一動點，在運動過程中，始終保持AM⊥MN，設BM=x,CN=y.
  （1）求出y與x的函數關系式，并寫出自變量x的取值范圍；
  （2）下表列出了部分點，先直接寫出m的值，然后在圖2中利用描點法畫出此函數圖象（注意邊界）；
  

  x	…	2	3	4	5	6	7	8	…
  y	…	2	2.7	3.2	3.5	m	3.5	3.2	…

  （3）結合圖象，指出M、N在運動過程中，當CN達到最大值時，BM的值是

  ；并寫出在整個運動過程中，點N運動的總路程

  ．
  組卷：579引用：2難度：0.4

  解析

• 23．在古代，智慧的勞動人民已經會使用“石磨”，其原理為在磨盤的邊緣連接一個固定長度的“連桿”，推動“連桿”帶動磨盤轉動，將糧食磨碎，物理學上稱這種動力傳輸工具為“曲柄連桿機構”．
  小明受此啟發設計了一個“雙連桿機構”，設計圖如圖1，兩個固定長度的“連桿”AP，BP的連接點P在⊙O上，當點P在⊙O上轉動時，帶動點A，B分別在射線OM，ON上滑動，OM⊥ON．當AP與⊙O相切時，點B恰好落在⊙O上，如圖2．請僅就圖2的情形解答下列問題．
  
  （1）求證：∠PAO=2∠PBO；
  （2）若⊙O的半徑為3，AP=4，求BP的長．
  組卷：654引用：9難度：0.5

  解析