滬教版高二（下）高考題單元試卷：第12章 圓錐曲線（09）

一、解答題（共30小題）

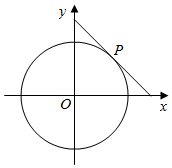• 1．圓x²+y²=4的切線與x軸正半軸，y軸正半軸圍成一個(gè)三角形，當(dāng)該三角形面積最小時(shí)，切點(diǎn)為P（如圖）．
  （Ⅰ）求點(diǎn)P的坐標(biāo)；
  （Ⅱ）焦點(diǎn)在x軸上的橢圓C過點(diǎn)P，且與直線l：y=x+

  3

  交于A、B兩點(diǎn)，若△PAB的面積為2，求C的標(biāo)準(zhǔn)方程．
  組卷：996引用：10難度：0.1

  解析

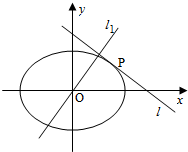• 2．如圖，設(shè)橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0），動(dòng)直線l與橢圓C只有一個(gè)公共點(diǎn)P，且點(diǎn)P在第一象限．
  （Ⅰ）已知直線l的斜率為k,用a,b,k表示點(diǎn)P的坐標(biāo)；
  （Ⅱ）若過原點(diǎn)O的直線l₁與l垂直，證明：點(diǎn)P到直線l₁的距離的最大值為a-b.
  組卷：2379引用：8難度：0.1

  解析

• 3．橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1，（a＞b＞0）的離心率

  2

  2

  ，點(diǎn)（2，

  2

  ）在C上．
  （1）求橢圓C的方程；
  （2）直線l不過原點(diǎn)O且不平行于坐標(biāo)軸，l與C有兩個(gè)交點(diǎn)A，B，線段AB的中點(diǎn)為M．證明：直線OM的斜率與l的斜率的乘積為定值．
  組卷：8076引用：37難度：0.3

  解析

• 4．設(shè)橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦點(diǎn)分別為F₁、F₂，右頂點(diǎn)為A，上頂點(diǎn)為B，已知|AB|=

  3

  2

  |F₁F₂|．
  （Ⅰ）求橢圓的離心率；
  （Ⅱ）設(shè)P為橢圓上異于其頂點(diǎn)的一點(diǎn)，以線段PB為直徑的圓經(jīng)過點(diǎn)F₁，經(jīng)過原點(diǎn)O的直線l與該圓相切，求直線l的斜率．
  組卷：2989引用：18難度：0.1

  解析

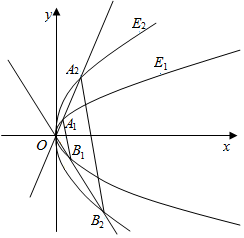• 5．如圖，已知兩條拋物線E₁：y²=2p₁x（p₁＞0）和E₂：y²=2p₂x（p₂＞0），過原點(diǎn)O的兩條直線l₁和l₂，l₁與E₁，E₂分別交于A₁、A₂兩點(diǎn)，l₂與E₁、E₂分別交于B₁、B₂兩點(diǎn)．
  （Ⅰ）證明：A₁B₁∥A₂B₂；
  （Ⅱ）過O作直線l（異于l₁，l₂）與E₁、E₂分別交于C₁、C₂兩點(diǎn)．記△A₁B₁C₁與△A₂B₂C₂的面積分別為S₁與S₂，求

  S

  1

  S

  2

  的值．
  組卷：1444引用：6難度：0.1

  解析

• 6．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）經(jīng)過點(diǎn)（0，

  3

  ），離心率為

  1

  2

  ，左、右焦點(diǎn)分別為F₁（-c,0），F(xiàn)₂（c,0）．
  （Ⅰ）求橢圓的方程；
  （Ⅱ）若直線l：y=-

  1

  2

  x+m與橢圓交于A、B兩點(diǎn)，與以F₁F₂為直徑的圓交于C、D兩點(diǎn)，且滿足

  |

  AB

  |

  |

  CD

  |

  =

  5

  3

  4

  ，求直線l的方程．
  組卷：3248引用：42難度：0.1

  解析

• 7．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左焦點(diǎn)為F（-2，0），離心率為

  6

  3

  ．
  （Ⅰ）求橢圓C的標(biāo)準(zhǔn)方程；
  （Ⅱ）設(shè)O為坐標(biāo)原點(diǎn)，T為直線x=-3上一點(diǎn)，過F作TF的垂線交橢圓于P、Q，當(dāng)四邊形OPTQ是平行四邊形時(shí)，求四邊形OPTQ的面積．
  組卷：1540引用：25難度：0.1

  解析

• 8．已知拋物線C：y²=2px（p＞0）的焦點(diǎn)為F，直線y=4與y軸的交點(diǎn)為P，與C的交點(diǎn)為Q，且|QF|=

  5

  4

  |PQ|．
  （Ⅰ）求C的方程；
  （Ⅱ）過F的直線l與C相交于A、B兩點(diǎn)，若AB的垂直平分線l′與C相交于M、N兩點(diǎn)，且A、M、B、N四點(diǎn)在同一圓上，求l的方程．
  組卷：3543引用：18難度：0.1

  解析

• 9．在平面直角坐標(biāo)系xOy中，橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  3

  2

  ，直線y=x被橢圓C截得的線段長(zhǎng)為

  4

  10

  5

  ．
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）過原點(diǎn)的直線與橢圓C交于A，B兩點(diǎn)（A，B不是橢圓C的頂點(diǎn)）．點(diǎn)D在橢圓C上，且AD⊥AB，直線BD與x軸、y軸分別交于M，N兩點(diǎn)．
  （i）設(shè)直線BD，AM的斜率分別為k₁，k₂，證明存在常數(shù)λ使得k₁=λk₂，并求出λ的值；
  （ii）求△OMN面積的最大值．
  組卷：2263引用：21難度：0.1

  解析

• 10．如圖，設(shè)橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦點(diǎn)分別為F₁，F(xiàn)₂，點(diǎn)D在橢圓上．DF₁⊥F₁F₂，

  丨

  F

  1

  F

  2

  丨

  丨

  D

  F

  1

  丨

  =2

  2

  ，△DF₁F₂的面積為

  2

  2

  ．
  （Ⅰ）求橢圓的標(biāo)準(zhǔn)方程；
  （Ⅱ）設(shè)圓心在y軸上的圓與橢圓在x軸的上方有兩個(gè)交點(diǎn)，且圓在這兩個(gè)交點(diǎn)處的兩條切線相互垂直并分別過不同的焦點(diǎn)，求圓的半徑．
  組卷：1498引用：12難度：0.1

  解析

一、解答題（共30小題）

• 29．已知橢圓x²+2y²=1，過原點(diǎn)的兩條直線l₁和l₂分別與橢圓交于點(diǎn)A、B和C、D，記△AOC的面積為S．
  （1）設(shè)A（x₁，y₁），C（x₂，y₂），用A、C的坐標(biāo)表示點(diǎn)C到直線l₁的距離，并證明S=

  1

  2

  |

  x

  1

  y

  2

  -

  x

  2

  y

  1

  |；
  （2）設(shè)l₁：y=kx,

  C

  （

  3

  3

  ，

  3

  3

  ）

  ，S=

  1

  3

  ，求k的值；
  （3）設(shè)l₁與l₂的斜率之積為m,求m的值，使得無(wú)論l₁和l₂如何變動(dòng)，面積S保持不變．
  組卷：2233引用：5難度：0.1

  解析

• 30．設(shè)橢圓中心在坐標(biāo)原點(diǎn)，A（2，0），B（0，1）是它的兩個(gè)頂點(diǎn)，直線y=kx（k＞0）與AB相交于點(diǎn)D，與橢圓相交于E、F兩點(diǎn)．
  （Ⅰ）若

  ED

  =

  6

  DF

  ，求k的值；
  （Ⅱ）求四邊形AEBF面積的最大值．
  組卷：4277引用：23難度：0.5

  解析