當前位置：試卷中心 > 試卷詳情

2023-2024學年福建省福州四中高二（上）期中數學試卷

發布：2024/10/10 3:0:1

一.單項選擇題（共8小題，每小題5分，共40分）

1．直線3x+2y-1=0的一個方向向量是（　　）
A．（2，-3） B．（2，3） C．（-3，2） D．（3，2）
組卷：1877引用：41難度：0.9
解析
2．雙曲線
x
2
4
-
y
2
9
=1的漸近線方程是（　　）
A．y=±
3
2
x B．y=±
2
3
x C．y=±
9
4
x D．y=±
4
9
x
組卷：728引用：21難度：0.7
解析
3．若直線（a+2）x+（1-a）y-3=0與直線（a-1）x+（2a+3）y+2=0互相垂直．則a的值為（　　）
A．1 B．-1 C．±1 D．-
3
2
組卷：335引用：17難度：0.9
解析
4．直線
x
4
+
y
2
=
1
與x軸，y軸分別交于點A，B，以線段AB為直徑的圓的方程為（　　）
A．x²+y²-4x-2y-1=0 B．x²+y²-4x-2y+1=0
C．x²+y²-4x-2y=0 D．x²+y²-2x-4y=0
組卷：500引用：10難度：0.7
解析
5．方程
（
x
-
2
）
2
+
y
2
+
（
x
+
2
）
2
+
y
2
=10，化簡的結果是（　　）
A．
x
2
25
+
y
2
16
=1 B．
x
2
25
+
y
2
21
=1
C．
x
2
25
+
y
2
4
=1 D．
y
2
25
+
x
2
21
=1
組卷：583引用：9難度：0.7
解析
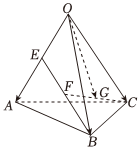6．如圖，四面體OABC中，點E為OA中點，F為BE中點，G為CF中點，設
OA
=
a
，
OB
=
b
，
OC
=
c
，若
OG
可用
a
，
b
，
c
表示為（　　）
A．
1
4
a
+
1
4
b
+
1
2
c
B．
1
8
a
+
1
4
b
+
1
2
c
C．
1
8
a
+
1
4
b
+
1
4
c
D．
1
8
a
+
1
8
b
+
1
2
c
組卷：127引用：5難度：0.5
解析
7．若橢圓
x
2
m
+
y
2
t
=
1
（
m
＞
t
＞
0
）
與雙曲線
x
2
n
-
y
2
t
=
1
（
n
＞
0
，
t
＞
0
）
有相同的焦點F₁，F₂，P是兩曲線的一個交點，則△F₁PF₂的面積是（　　）
A．
t
2
B．t C．2t D．4t
組卷：126引用：3難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（共6小題）

21．已知F₁是橢圓
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左焦點，上頂點B的坐標是
（
0
，
2
）
，離心率為
6
3
．
（1）求橢圓的標準方程；
（2）O為坐標原點，直線l過點F₁且與橢圓相交于P，Q兩點，過點F₁作EF₁⊥PQ，與直線x=-3相交于點E，連接OE，與線段PQ相交于點M，求證：點M為線段PQ的中點．
組卷：80引用：2難度：0.4
解析
22．如圖，在平面直角坐標系xOy中，已知以M為圓心的圓M：x²+y²-12x-14y+60=0及其上一點A（2，4）．
（1）設圓N與x軸相切，與圓M外切，且圓心N在直線x=6上，求圓N的標準方程；
（2）設平行于OA的直線l與圓M相交于B，C兩點，且|BC|=|OA|，求直線l的方程；
（3）設點T（t,0）滿足：存在圓M上的兩點P和Q，使得
TA
+
TP
=
TQ
，求實數t的取值范圍．
組卷：527引用：15難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．x²+y²-4x-2y-1=0	B．x²+y²-4x-2y+1=0
C．x²+y²-4x-2y=0	D．x²+y²-2x-4y=0

A． x 2 25 + y 2 16 =1	B． x 2 25 + y 2 21 =1
C． x 2 25 + y 2 4 =1	D． y 2 25 + x 2 21 =1

A． 1 4 a + 1 4 b + 1 2 c	B． 1 8 a + 1 4 b + 1 2 c
C． 1 8 a + 1 4 b + 1 4 c	D． 1 8 a + 1 8 b + 1 2 c

2023-2024學年福建省福州四中高二（上）期中數學試卷

一.單項選擇題（共8小題，每小題5分，共40分）

1．直線3x+2y-1=0的一個方向向量是（ ）

2．雙曲線x24-y29=1的漸近線方程是（ ）

3．若直線（a+2）x+（1-a）y-3=0與直線（a-1）x+（2a+3）y+2=0互相垂直．則a的值為（ ）

4．直線x4+y2=1與x軸，y軸分別交于點A，B，以線段AB為直徑的圓的方程為（ ）

5．方程（x-2）2+y2+（x+2）2+y2=10，化簡的結果是（ ）

6．如圖，四面體OABC中，點E為OA中點，F為BE中點，G為CF中點，設OA=a，OB=b，OC=c，若OG可用a，b，c表示為（ ）

7．若橢圓x2m+y2t=1（m＞t＞0）與雙曲線x2n-y2t=1（n＞0，t＞0）有相同的焦點F1，F2，P是兩曲線的一個交點，則△F1PF2的面積是（ ）

四、解答題（共6小題）

1．直線3x+2y-1=0的一個方向向量是（　　）

2．雙曲線
x
2
4
-
y
2
9
=1的漸近線方程是（　　）

3．若直線（a+2）x+（1-a）y-3=0與直線（a-1）x+（2a+3）y+2=0互相垂直．則a的值為（　　）

4．直線
x
4
+
y
2
=
1
與x軸，y軸分別交于點A，B，以線段AB為直徑的圓的方程為（　　）

5．方程
（
x
-
2
）
2
+
y
2
+
（
x
+
2
）
2
+
y
2
=10，化簡的結果是（　　）

6．如圖，四面體OABC中，點E為OA中點，F為BE中點，G為CF中點，設
OA
=
a
，
OB
=
b
，
OC
=
c
，若
OG
可用
a
，
b
，
c
表示為（　　）

7．若橢圓
x
2
m
+
y
2
t
=
1
（
m
＞
t
＞
0
）
與雙曲線
x
2
n
-
y
2
t
=
1
（
n
＞
0
，
t
＞
0
）
有相同的焦點F₁，F₂，P是兩曲線的一個交點，則△F₁PF₂的面積是（　　）