2022-2023學年河北省廊坊市霸州市部分學校九年級（上）期末數學試卷

一、單項選擇題：共14題，1-8題每題3分，9-14題每題2分，共36分。在每小題給出的四個選項中，只有一個是符合題目要求的。

• 1．在解一元二次方程x²+px+q=0時，小紅看錯了常數項q,得到方程的兩個根是-3，1．小明看錯了一次項系數p,得到方程的兩個根是5，-4，則原來的方程是（　　）

  A．x2+2x-3=0

  B．x2+2x-20=0

  C．x2-2x-20=0

  D．x2-2x-3=0
  組卷：3320引用：24難度：0.6

  解析

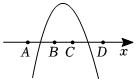• 2．已知二次函數y=-x²+bx+c的圖象如圖所示，并有以下結論：①函數圖象與y軸正半軸相交；②當x＜0時，y隨x的增大而增大，則坐標系的原點O可能是（　　）

  A．點A

  B．點B

  C．點C

  D．點D
  組卷：227引用：5難度：0.5

  解析

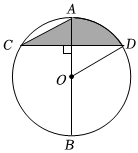• 3．如圖，AB是⊙O的直徑，弦CD⊥AB，∠C=30°，CD=2

  3

  ，則陰影部分圖形的面積為（　　）

  A．4π

  B．2π

  C．π

  D． 2 π 3
  組卷：222引用：1難度：0.6

  解析

• 4．如圖，若拋物線y=-x²+3與x軸圍成封閉區域（邊界除外）內整點（點的橫、縱坐標都是整數）的個數為k,則反比例函數y=

  k

  x

  （x＞0）的圖象是（　　）

  A．

  B．

  C．

  D．
  組卷：135引用：2難度：0.6

  解析

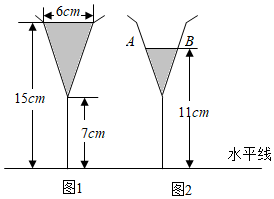• 5．圖1是裝了液體的高腳杯示意圖（數據如圖），用去一部分液體后如圖2所示，此時液面AB=（　　）

  A．1cm

  B．2cm

  C．3cm

  D．4cm
  組卷：3875引用：52難度：0.5

  解析

• 6．已知：島P位于島Q的正西方，由島P，Q分別測得船R位于南偏東30°和南偏西45°方向上，符合條件的示意圖是（　　）

  A．	B．
  C．	D．
  組卷：7109引用：78難度：0.9

  解析

• 7．已知正方形MNOK和正六邊形ABCDEF邊長均為1，把正方形放在正六邊形中，使OK邊與AB邊重合，如圖所示，按下列步驟操作：
  將正方形在正六邊形中繞點B順時針旋轉，使KM邊與BC邊重合，完成第一次旋轉；再繞點C順時針旋轉，使MN邊與CD邊重合，完成第二次旋轉；…在這樣連續6次旋轉的過程中，點B，M間的距離可能是（　　）

  A．1.4

  B．1.1

  C．0.8

  D．0.5
  組卷：2591引用：13難度：0.3

  解析

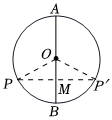• 8．已知AB是⊙O的任意一條直徑，求證：⊙O是以直徑AB所在直線為對稱軸的軸對稱圖形．下列為證明過程，嘉琪為保證推理更嚴謹，想在方框中“∵OP=OP′，”和“∴PM=MP′，”之間做補充，下列敘述正確的是（　　）
  證明：如圖，設點P是⊙O上除點A、B以外任意一點，
  過點P作PP′⊥AB，交⊙O于點P′，垂足為點M，
  若點M與圓心O不重合，
  連接OP，OP′，在△OPP′中，∵OP=OP′，∴PM=MP′，則AB是PP′的垂直平分線，
  若點M與圓心O重合，顯然AB是PP′的垂直平分線，
  ∴對于圓上任意一點P，在圓上都有關于直線AB的對稱點P′
  ∴⊙O是以直徑AB所在直線為對稱軸的軸對稱圖形．

  A．推理嚴謹，不必補充

  B．應補充：∴△OPP′是等腰三角形

  C．應補充：又∵PP′⊥AB

  D．應補充：∴△OPP′是等腰三角形，又∵PP′⊥AB
  組卷：37引用：3難度：0.7

  解析

三、解答題：共5題，共52分，解答應寫出必要的文字說明、證明過程或演算步驟。

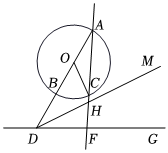• 23．如圖，延長⊙O的直徑AB，交直線DG于點D，且BD=

  1

  2

  AB=10，∠ADG=60°．射線DM從DG出發繞點D逆時針旋轉，旋轉角為α；同時，線段OC從OB出發繞點O逆時針旋轉，旋轉角為2α，直線AC與射線DM相交于點H，與直線DG相交于點F，其中0°＜α＜180°，且α≠90°．
  （1）當α=20°時，弧BC的長為

  ；
  （2）當α=120°時，判斷△ADH的形狀，并求它的周長；
  （3）△ADH的外心能否在邊DH上，如果能，求出α的度數；如果不能，請說明理由；
  （4）若射線DM與⊙O有公共點，直接寫出α的取值范圍；
  （5）當tan∠BAC=

  3

  5

  時，求線段HF的長度．
  組卷：173引用：3難度：0.1

  解析

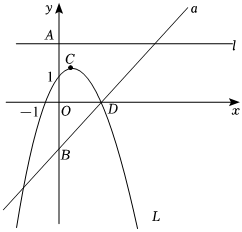• 24．如圖，若b是正數，直線l：y=b與y軸交于點A；直線a：y=x-b與y軸交于點B；拋物線L：y=-x²+bx的頂點為C，且L與x軸正半軸的交點為D．
  （1）若AB=8，求b的值，并求此時L的對稱軸與a的交點坐標；
  （2）當點C在l下方時，求點C與l距離的最大值；
  （3）設x₀≠0，點（x₀，y₁），（x₀，y₂），（x₀，y₃）分別在l,a和L上，且y₃是y₁，y₂的平均數，求點（x₀，0）與點D間的距離；
  （4）在L和a所圍成的封閉圖形的邊界上，把橫、縱坐標都是整數的點稱為“美點”，分別直接寫出b=2019和b=2019.5時“美點”的個數．
  組卷：264引用：2難度：0.2

  解析