2022-2023學(xué)年福建省廈門市思明區(qū)湖濱中學(xué)八年級(jí)（下）期末數(shù)學(xué)試卷
發(fā)布：2024/6/6 8:0:9
一、選擇題（本大題共10小題．每小題4分，共40分．每小題只有一個(gè)選項(xiàng)符合題意）
-
1．若二次根式
有意義，則x的取值可能是（ ）x-3組卷：35引用：2難度：0.7 -
2．下列各組數(shù)據(jù)中，不能作為直角三角形邊長(zhǎng)的是（ ）
組卷：101引用：3難度：0.7 -
3．用配方法解方程x2-2x-5=0方程可變形為（ ）
組卷：474引用：8難度：0.9 -
4．直線y=-3x+1不經(jīng)過第（ ）象限．
組卷：204引用：7難度：0.9 -
5．一個(gè)正方形的面積是15，估計(jì)它的邊長(zhǎng)大小在（ ）
組卷：1673引用：136難度：0.9 -
6．某校八年（2）班8位男生的身高（單位：cm）分別為：163，a,167，167，167，164，172，166，其中167一定是這組數(shù)據(jù)的（ ）
組卷：56引用：3難度：0.7 -
7．對(duì)于一次函數(shù)y=-2x+4，當(dāng)-2≤x≤4時(shí)，函數(shù)y的取值范圍是（ ）
組卷：631引用：6難度：0.7 -
8．若面積為6菱形的一對(duì)角線長(zhǎng)為
，則另一對(duì)角線長(zhǎng)為（ ）22組卷：325引用：4難度：0.7
三、解答題（本大題共9小題，共86分）
-
24．如圖1，在正方形ABCD中，E是邊AB上的一動(dòng)點(diǎn)（不與B重合），EH⊥DE，EH=DE，DH交BC于點(diǎn)G，連接BH．
（1）若AD=4，E為AB的中點(diǎn)，請(qǐng)直接寫出線段DE和DH的長(zhǎng)度．DE=，DH=．
（2）探究線段BH與AE的數(shù)量關(guān)系，并給出證明．
（3）如圖2，連接EG，比較∠GEH和∠BEH的大小關(guān)系，并說明理由．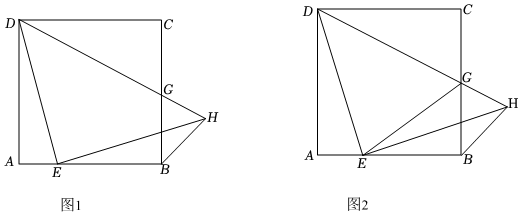
組卷：373引用：3難度：0.2 -
25．6月份，福建多地暴雨連連，根據(jù)天氣預(yù)報(bào)，6月6日起，廈門將持續(xù)下雨7天，廈門某水庫A記錄了6月6日24小時(shí)內(nèi)的水位變化情況，結(jié)果如下：
在不泄洪的條件下，假設(shè)下雨的這7天水位隨時(shí)間的變化都滿足這種關(guān)系．為了保護(hù)大壩安全，當(dāng)水庫的水位達(dá)到43m時(shí)，必須進(jìn)行泄洪．與此同時(shí)，西部某地區(qū)由于干旱，需要抽調(diào)某水庫B中的水作為生活用水，這7天內(nèi)（含7天）的水位y（單位：m）隨時(shí)間x（單位：h）變化情況如圖所示．時(shí)刻 0：00 5：00 10：00 15：00 20：00 … 水位g/m 40 40.125 40.25 40.375 40.5 …
（1）在不泄洪的條件下，寫出一個(gè)函數(shù)解析式描述水位g（單位：m）隨時(shí)間x（單位：h）的變化規(guī)律；
（2）當(dāng)水庫A需要進(jìn)行泄洪時(shí)，若為了更快速降低水位，多開了幾個(gè)泄洪閘，使水位平均每小時(shí)下降0.275m,則在這7天內(nèi)（含7天），是否存在某個(gè)時(shí)刻，兩個(gè)水庫的水位差距與一開始相同？若有，求出此時(shí)水庫B的水位；若無，說明理由．
（3）假設(shè)泄洪的速度一定，當(dāng)水庫A泄洪后的第20小時(shí)起，水庫A的水位始終不超過水庫B的水位，請(qǐng)問：水庫A最遲能否在第6天早上6點(diǎn)前降至原水位？組卷：254引用：3難度：0.4