2023-2024學(xué)年黑龍江省齊齊哈爾市龍江縣五校聯(lián)考九年級(jí)（上）第一次月考數(shù)學(xué)試卷

一.單項(xiàng)選擇題（每題3分，共30分）

• 1．將下列一元二次方程化成一般形式后，其中二次項(xiàng)系數(shù)是3，一次項(xiàng)系數(shù)是-6，常數(shù)項(xiàng)是1的方程是（　　）

  A．3x2+1=6x

  B．3x2-1=6x

  C．3x2+6x=1

  D．3x2-6x=1
  組卷：1487引用：10難度：0.8

  解析

• 2．用配方法解方程x²+8x+9=0，變形后的結(jié)果正確的是（　　）

  A．（x+4）2=-9

  B．（x+4）2=-7

  C．（x+4）2=25

  D．（x+4）2=7
  組卷：885引用：11難度：0.7

  解析

• 3．在某籃球邀請(qǐng)賽中，參賽的每?jī)蓚€(gè)隊(duì)之間都要比賽一場(chǎng)，共比賽36場(chǎng)．設(shè)有x個(gè)隊(duì)參賽，根據(jù)題意，可列方程為（　　）

  A． 1 2 x（x-1）=36	B． 1 2 x（x+1）=36
  C．x（x-1）=36	D．x（x+1）=36
  組卷：3635引用：44難度：0.8

  解析

• 4．若關(guān)于x的一元二次方程x（x-1）+bx=0有兩個(gè)相等的實(shí)數(shù)根，則實(shí)數(shù)b的值為（　　）

  A．-1

  B．1

  C．-2或2

  D．-3或1
  組卷：433引用：4難度：0.7

  解析

• 5．二次函數(shù)y=（x-2）²+3的圖象的頂點(diǎn)坐標(biāo)是（　　）

  A．（2，3）

  B．（-2，3）

  C．（-2，-3）

  D．（2，-3）
  組卷：3239引用：34難度：0.6

  解析

• 6．與y=2x²+3x+1形狀相同的拋物線解析式為（　　）

  A．y=1+ 1 2 x2

  B．y=（2x+1）2

  C．y=（x-1）2

  D．y=-2x2
  組卷：396引用：7難度：0.6

  解析

• 7．已知點(diǎn)A（1，y₁），B（2，y₂），C（0，y₃）在拋物線y=-（x+1）²+2上，則下列結(jié)論正確的是（　　）

  A．y3＞y2＞y1

  B．y3＞y1＞y2

  C．y1＞y2＞y3

  D．y2＞y1＞y3
  組卷：179引用：2難度：0.6

  解析

• 8．函數(shù)y=ax²與y=ax+a（a＜0）在同一平面直角坐標(biāo)系內(nèi)圖象大致是（　　）

  A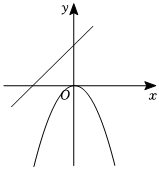．	B．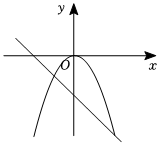
  C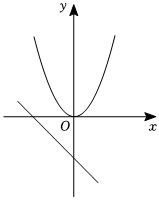．	D．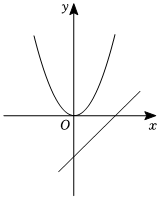
  組卷：978引用：3難度：0.5

  解析

三.解答題（63分）

• 23．某超市銷售櫻桃，已知櫻桃的進(jìn)價(jià)為14元/千克，如果售價(jià)為20元/千克，那么每天可售出260千克，如果售價(jià)為25元/千克，那么每天可售出210千克，經(jīng)調(diào)查發(fā)現(xiàn)：每天的銷售量y（千克）與售價(jià)x（元/千克）之間存在一次函數(shù)關(guān)系
  （1）求y與x之間的函數(shù)關(guān)系式；
  （2）若該超市每天要獲得利潤(rùn)1920元，同時(shí)又要讓消費(fèi)者得到實(shí)惠，則售價(jià)x應(yīng)定于多少元？
  （3）若櫻桃的售價(jià)不得高于28元/千克，請(qǐng)問(wèn)售價(jià)定為多少時(shí)，該超市每天銷售櫻桃所獲的利潤(rùn)最大？最大利潤(rùn)是多少元？
  組卷：413引用：5難度：0.6

  解析

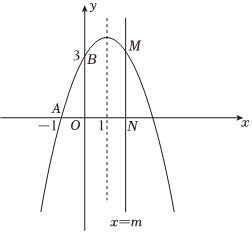• 24．在平面直角坐標(biāo)系中，拋物線y=ax²+bx+c（a≠0）經(jīng)過(guò)點(diǎn)A（-1，0）和B（0，3），其頂點(diǎn)的橫坐標(biāo)為1．
  （1）求拋物線的表達(dá)式．
  （2）若直線x=m與x軸交于點(diǎn)N，在第一象限內(nèi)與拋物線交于點(diǎn)M，當(dāng)m取何值時(shí)，使得AN+MN有最大值，并求出最大值．
  （3）若點(diǎn)P為拋物線y=ax²+bx+c（a≠0）的對(duì)稱軸上一動(dòng)點(diǎn)，將拋物線向左平移1個(gè)單位長(zhǎng)度后，Q為平移后拋物線上一動(dòng)點(diǎn)．在（2）的條件下求得的點(diǎn)M，是否能與A、P、Q構(gòu)成平行四邊形？若能構(gòu)成，求出Q點(diǎn)坐標(biāo)；若不能構(gòu)成，請(qǐng)說(shuō)明理由．
  組卷：2404引用：4難度：0.2

  解析