2022-2023學年廣東省深圳市寶安區海旺中學七年級（下）期中數學試卷

一.選擇題（共10題，每小題3分，共30分）

• 1．3^-2=（　　）

  A． 1 6

  B． 1 9

  C．-6

  D．-9
  組卷：255引用：5難度：0.7

  解析

• 2．下列計算中，結果正確的是（　　）

  A．a2?a3=a6	B．（a2）10=a20
  C．（2a）（3a）=6a	D．a12÷a2=a6
  組卷：289引用：5難度：0.7

  解析

• 3．華為Mate20手機搭載了全球首款7納米制程芯片，7納米就是0.000000007米．數據0.000000007用科學記數法表示為（　　）

  A．7×10-9

  B．0.7×10-8

  C．7×10-8

  D．7×10-7
  組卷：339引用：3難度：0.9

  解析

• 4．用一塊含30°角的透明直角三角板畫已知△ABC的邊BC上的高，下列三角板的擺放位置正確的是（　　）

  A．

  B．

  C．

  D．
  組卷：3318引用：19難度：0.7

  解析

• 5．如圖，在大燒杯中放了一個小燒杯，現向小燒杯中勻速注水，小燒杯滿了后繼續勻速注水，則大燒杯的液面高度h（cm）與時間注水時間t（s）的大致圖象是（　　）

  A．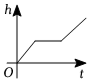

  B．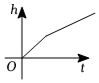

  C．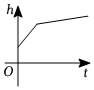

  D．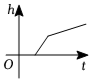
  組卷：1952引用：15難度：0.7

  解析

• 6．下列說法正確的有（　　）
  ①不相交的兩條直線是平行線；
  ②經過直線外一點，有且只有一條直線與這條直線平行；
  ③兩條直線被第三條直線所截，同旁內角互補；
  ④在同一平面內，若直線a⊥b,b⊥c,則直線a∥c.

  A．4個

  B．3個

  C．2個

  D．1個
  組卷：658引用：4難度：0.7

  解析

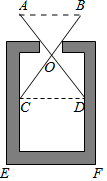• 7．在測量一個小口圓形容器的壁厚（厚度均勻）時，小明用“X型轉動鉗”按如圖方法進行測量，其中OA=OD，OB=OC，測得AB=3厘米，EF=4厘米，圓形容器的壁厚是（　　）

  A．2厘米

  B．1.5厘米

  C．1厘米

  D．0.5厘米
  組卷：850引用：5難度：0.7

  解析

三.解答題（共7小題，共55分.）

• 21．【項目學習】配方法是數學中重要的一種思想方法，它是指將一個式子的某部分通過恒等變形化為完全平方式或幾個完全平方式的和的方法，這種方法常被用到代數式的變形中，并結合非負數的意義來解決一些問題．
  例如，把二次三項式x²-2x+3進行配方
  解：x²-2x+3=x²-2x+1+2=（x²-2x+1）+2=（x-1）²+2
  我們定義：一個整數能表示成a²+b²（a,b是整數）的形式，則稱這個數為“完美數”．例如，5是“完美數”，理由：因為5=2²+1²，再如，M=x²+2xy+2y²=（x+y）²+y²，（x,y是整數）所以M也是“完美數”
  【問題解決】
  （1）下列各數中，“完美數”有

  ．（填序號）
  ①10
  ②45
  ③28
  ④29
  （2）若二次三項式x²-6x+13（x是整數）是“完美數”，可配方成（x-m）²+n（m,n為常數），則mn的值為

  ；
  【問題探究】
  （3）已知S=x²+9y²+8x-12y+k（x,y是整數，k是常數），要使S為“完美數”，試求出符合條件的k的值．
  【問題拓展】
  （4）已知實數x,y滿足-x²+7x+y-10=0，求x+y的最小值．
  組卷：1154引用：4難度：0.6

  解析

• 22．【問題情境】：
  課外數學興趣小組活動時，老師提出了如下何題：
  如圖①，△ABC中，若AB=10，AC=6，求BC邊上的中線AD的取值范圍．
  小明在組內經過合作交流，得到了如下的解決方法：延長AD至點E，使DE=AD，連接BE，請根據小明的方法思考：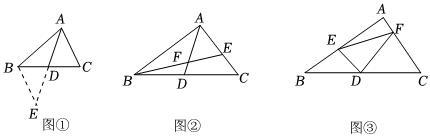
  
  （1）由已知和作圖能得到△ADC≌△EDB，依據是

  ．
  A．SSS B．SAS C．AAS  D．SSA
  （2）由“三角形的三邊關系”可求得AD的取值范圍是

  ．
  解后反思：題目中出現“中點”、“中線”等條件，可考慮延長中線構造全等三角形，把分散的已知條件和所求證的結論集中到同一個三角形之中．
  【初步運用】：
  （3）如圖②，AD是△ABC的中線，BE交AC于E，交AD于F，且AE=EF．若EF=5，EC=3，求線段BF的長．
  【拓展提升】：
  （4）如圖③，在△ABC中，D為BC的中點，DE⊥DF分別交AB，AC于點E，F．求證：BE+CF＞EF．
  組卷：597引用：2難度：0.1

  解析