2022-2023學年河北省衡水中學高三（上）第一次調研數學試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合A={x|x²-3x＜0}，

  B

  =

  {

  x

  |

  3

  x

  ≥

  3

  }

  ，則A∩B=（　　）

  A． （ 0 ， 1 2 ）

  B． [ 1 2 ， 3 ）

  C． （ 0 ， 2 ）

  D．（1，3）
  組卷：118引用：7難度：0.8

  解析

• 2．若a=5^0.1，

  b

  =

  1

  2

  lo

  g

  2

  3

  ，c=log₃0.8，則a,b,c的大小關系為（　　）

  A．a＞b＞c

  B．b＞a＞c

  C．c＞b＞a

  D．c＞a＞b
  組卷：277引用：6難度：0.7

  解析

• 3．設a,b∈R，則使a＞b成立的一個充分不必要條件是（　　）

  A．a3＞b3	B． 1 a ＜ 1 b
  C．a2＞b2	D．log2（a-b）＞0
  組卷：71引用：11難度：0.7

  解析

• 4．我國古代數學家李善蘭在《對數探源》中利用尖錐術理論來制作對數表，他通過“對數積”求得ln2≈0.693，

  ln

  5

  4

  ≈0.223，由此可知ln0.2的近似值為（　　）

  A．-1.519

  B．-1.726

  C．-1.609

  D．-1.316
  組卷：97引用：3難度：0.7

  解析

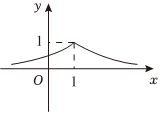• 5．已知y關于x的函數圖象如圖所示，則實數x,y滿足的關系式可以是（　　）

  A． | x - 1 | - lo g 3 1 y = 0	B． 2 x - 1 = x 3 y
  C．2|x-1|-y=0	D．ln|x|=y-1
  組卷：29引用：1難度：0.5

  解析

• 6．已知函數f（x）是定義在R上的單調函數．若對任意x∈R，都有f[f（x）-2^x]=3，則f（4）=（　　）

  A．9

  B．15

  C．17

  D．33
  組卷：41引用：3難度：0.8

  解析

• 7．函數f（x）=

  6

  e

  x

  +

  1

  +

  mx

  |

  x

  |

  +

  1

  的最大值為M，最小值為N，則M+N=（　　）

  A．3

  B．4

  C．6

  D．與m值有關
  組卷：209引用：6難度：0.6

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．經過市場調研發現，某企業生產的某種時令商品在未來一個月（30天）內的日銷售量m（t）（單位：百件）與時間第t天的關系如下表所示：
  

  第t天	1	3	10	…	30
  日銷售量m（t）/百件	2	3	6.5	…	16.5

  未來30天內，受市場因素影響，前15天此商品每天每件的利潤f₁（t）（單位：元）與時間第t天的函數關系式為f₁（t）=-3t+88（1≤t≤15，且t∈Z），而后15天此商品每天每件的利潤f₂（t）（單位：元）與時間第t天的函數關系式為f₂（t）=

  600

  t

  +

  2

  （

  16

  ≤

  t

  ≤

  30

  ，且t∈Z）．
  （1）現給出以下兩類函數模型：①m（t）=kt+b（k,b為常數）；②m（t）=b?a^t（a,b為常數，a＞0，且a≠1）．分析表格中的數據，請說明應選擇哪類函數模型，并求出該函數模型的解析式；
  （2）若這30天內該企業此商品的日銷售利潤均未能超過40000元，則考慮轉型．請判斷該企業是否需要考慮轉型，并說明理由．
  組卷：13引用：1難度：0.6

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  1 x - 1 ， 0 ＜ x ＜ 1

  （ x - 1 ） 2 ， x ≥ 1

  ．
  （1）當0＜a＜b,且f（a）=f（b）時，求

  （

  1

  a

  ）

  2

  +（b-1）²的取值范圍；
  （2）是否存在正實數a,b（a＜b），使得函數y=f（x）在[a,b]上的取值范圍是[a-1，b-1]．若存在，則求出a,b的值；若不存在，請說明理由．
  組卷：111引用：3難度：0.4

  解析