2022-2023學年河北省滄州市高二（下）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合

  A

  =

  {

  x

  |

  y

  =

  3

  -

  x

  ，

  B

  =

  {

  1

  ，

  2

  ，

  3

  ，

  4

  }

  ，則A∩B=（　　）

  A．{3}

  B．{2，3}

  C．{1，2，3}

  D．{1，2，3，4}
  組卷：90引用：3難度：0.8

  解析

• 2．設a,b∈R，則“（a-b）a²＞0”是“a＞b”的（　　）

  A．必要不充分條件	B．充分不必要條件
  C．既不充分也不必要條件	D．充要條件
  組卷：160引用：6難度：0.9

  解析

• 3．在某項測試中，測量結果X～N（1，σ²）（σ＞0），若P（1＜X＜2）=0.3，則P（X≤0）=（　　）

  A．0.1

  B．0.2

  C．0.3

  D．0.4
  組卷：35引用：2難度：0.8

  解析

• 4．觀察下列四幅殘差圖，滿足一元線性回歸模型中對隨機誤差的假定的是（　　）

  A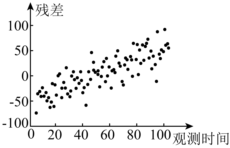．	B．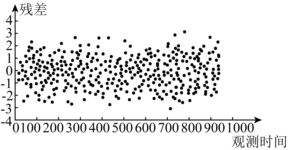
  C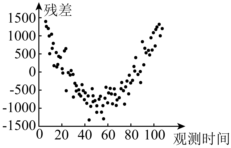．	D．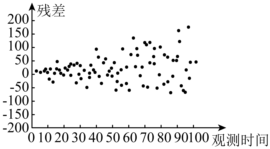
  組卷：238引用：6難度：0.8

  解析

• 5．設隨機變起X的分布列為

  P

  （

  X

  =

  i

  ）

  =

  k

  2

  i

  （

  i

  =

  1

  ，

  2

  ，

  3

  ，

  4

  ）

  ，則P（X≤2）=（　　）

  A． 8 15

  B． 4 15

  C． 4 5

  D． 2 5
  組卷：131引用：2難度：0.7

  解析

• 6．已知f（x）為定義在R上的奇函數，f（1）=2，若?x₁，x₂∈（0，+∞）（x₁≠x₂）總有

  （

  x

  1

  -

  x

  2

  ）

  ?

  [

  f

  （

  x

  1

  ）

  x

  1

  -

  f

  （

  x

  2

  ）

  x

  2

  ]

  ＜

  0

  ．則不等式f（x+3）＞2x+6的解集為（　　）

  A．（-∞，-4）	B．（2，3）
  C．（-∞，-4）∪（-3，-2）	D．（-∞，-4）∪（2，3）
  組卷：88引用：5難度：0.6

  解析

• 7．將4本不同的書全部分給3個同學，每人至少一本，且1號書不能給甲同學，則不同的分法種數為（　　）

  A．6

  B．12

  C．18

  D．24
  組卷：158引用：3難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．端午假日期間，某商場為了促銷舉辦了購物砸金蛋活動，凡是在該商場購物的顧客都有一次砸金蛋的機會．主持人從編號為1，2，3，4的四個金蛋中隨機選擇一個，放入獎品，只有主持人事先知道獎品在哪個金蛋里．游戲規則是顧客有兩次選擇機會，第一次任意選一個金蛋先不砸開，隨后主持人隨機砸開另外三個金蛋中的一個空金蛋，接下來顧客從三個完好的金蛋中第二次任意選擇一個砸開，如果砸中有獎的金蛋直接獲獎．現有顧客甲第一次選擇了2號金蛋，接著主持人砸開了另外三個金蛋中的一個空金蛋．
  （1）作為旁觀者，請你計算主持人砸4號金蛋的概率；
  （2）當主持人砸開4號金蛋后，顧客甲重新選擇，請問他是堅持選2號金蛋，還是改選1號金蛋或3號金蛋？（以獲得獎品的概率最大為決策依據）
  組卷：84引用：3難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  t

  +

  lnx

  lnx

  -

  1

  （

  t

  ≠

  -

  1

  ）

  ，且滿足

  f

  （

  x

  ）

  f

  （

  1

  x

  ）

  =

  1

  ．
  （1）當x≥e²時，求f（x）的值域；
  （2）設a,b∈（e,+∞），且f（a）+f（b）=4，求f（ab）的最大值．
  組卷：9引用：2難度：0.5

  解析