2022-2023學(xué)年江蘇省鹽城市東臺實驗中學(xué)九年級(下)期中數(shù)學(xué)試卷
發(fā)布:2024/4/20 14:35:0
一、選擇題(本大題共8小題,每小題3分,共24分)
-
1.2023的相反數(shù)是( )
A. 12023B. -12023C.2023 D.-2023 組卷:5354引用:291難度:0.8 -
2.要使得式子
有意義,則x的取值范圍是( )x-2A.x>2 B.x≥2 C.x<2 D.x≤2 組卷:275引用:19難度:0.8 -
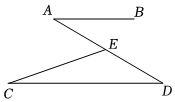 3.如圖,已知AB∥CD,點E在線段AD上(不與點A,點D重合),連接CE.若∠C=20°,∠AEC=50°,則∠A=( )
3.如圖,已知AB∥CD,點E在線段AD上(不與點A,點D重合),連接CE.若∠C=20°,∠AEC=50°,則∠A=( )A.10° B.20° C.30° D.40° 組卷:1299引用:36難度:0.7 -
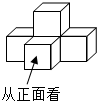 4.如圖是由5個相同的正方體搭成的立體圖形,則它的主視圖為( )
4.如圖是由5個相同的正方體搭成的立體圖形,則它的主視圖為( )A. 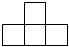
B. 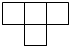
C. 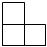
D. 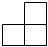 組卷:616引用:15難度:0.8
組卷:616引用:15難度:0.8 -
5.下列運算正確的是( )
A.a(chǎn)3?a2=a6 B.a(chǎn)6÷a2=a3 C.2a+4b=8ab D.(a2)3=a6 組卷:64引用:3難度:0.8 -
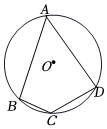 6.如圖,四邊形ABCD為⊙O的內(nèi)接四邊形,若∠A=50°,則∠BCD的度數(shù)為( )
6.如圖,四邊形ABCD為⊙O的內(nèi)接四邊形,若∠A=50°,則∠BCD的度數(shù)為( )A.50° B.80° C.100° D.130° 組卷:538引用:7難度:0.6 -
7.關(guān)于x的一元二次方程x2+2x+k=0有兩個相等的實數(shù)根,則k的取值范圍是( )
A.k=-1 B.k>-1 C.k=1 D.k>1 組卷:676引用:9難度:0.9 -
8.我國古代數(shù)學(xué)名著《九章算術(shù)》中記載:“粟米之法:粟率五十;糲米三十.今有米在十斗桶中,不知其數(shù).滿中添粟而舂之,得米七斗.問故米幾何?”意思為:50斗谷子能出30斗米,即出米率為
.今有米在容量為10斗的桶中,但不知道數(shù)量是多少.再向桶中加滿谷子,再舂成米,共得米7斗.問原來有米多少斗?如果設(shè)原來有米x斗,向桶中加谷子y斗,那么可列方程組為( )35A. x+y=10x+35y=7B. x+y=1035x+y=7C. x+y=7x+53y=10D. x+y=753x+y=10組卷:2139引用:28難度:0.7
二、填空題(本大題共8小題,每小題3分,共24分)
-
9.一組數(shù)據(jù)2,0,1,2,6中,眾數(shù)是 .
組卷:26引用:1難度:0.7
三、解答題(本大題共有11小題,共102分.請在答題卡指定區(qū)域內(nèi)作答,解答時應(yīng)寫出文字說明、推理過程或演算步驟)
-
26.定義:我們知道,四邊形的一條對角線把這個四邊形分成了兩個三角形,如果這兩個三角形相似(不全等),我們就把這條對角線叫做這個四邊形的“相似對角線”.
(1)如圖1,△ABC的三個頂點均在正方形網(wǎng)格中的格點上,若四邊形ABCD是以AC為“相似對角線”的四邊形,請只用無刻度的直尺,就可以在網(wǎng)格中畫出點D,請你在圖1中找出滿足條件的點D,保留畫圖痕跡(找出2個即可)
(2)①如圖2,在四邊形ABCD中,∠DAB=90°,∠DCB=135°,對角線AC平分∠DAB.請問AC是四邊形ABCD的“相似對角線”嗎?請說明理由;
②若AC=,求AD?AB的值.10
(3)如圖3,在(2)的條件下,若∠D=∠ACB=90°時,將△ADC以A為位似中心,位似比為:5縮小得到△AEF,連接CE、BF,在△AEF繞點A旋轉(zhuǎn)的過程中,當(dāng)CE所在的直線垂直于AF時,請你直接寫出BF的長.2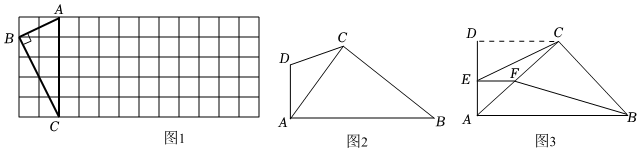 組卷:918引用:4難度:0.3
組卷:918引用:4難度:0.3 -
27.定義:若兩個函數(shù)的圖象關(guān)于某一點P中心對稱,則稱這兩個函數(shù)關(guān)于點P互為“伴隨函數(shù)”.例如,函數(shù)y=x2與y=-x2關(guān)于原點O互為“伴隨函數(shù)”.
(1)函數(shù)y=x+1關(guān)于原點O的“伴隨函數(shù)”的函數(shù)解析式為 ,函數(shù)y=(x-2)2+1關(guān)于原點O的“伴隨函數(shù)”的函數(shù)解析式為 ;
(2)已知函數(shù)y=x2-2x與函數(shù)G關(guān)于點P(m,3)互為“伴隨函數(shù)”.若當(dāng)m<x<7時,函數(shù)y=x2-2x與函數(shù)G的函數(shù)值y都隨自變量x的增大而增大,求m的取值范圍;
(3)已知點A(0,1),點B(4,1),點C(2,0),二次函數(shù)y=ax2-2ax-3a(a>0)與函數(shù)N關(guān)于點C互為“伴隨函數(shù)”,將二次函數(shù)y=ax2-2ax-3a(a>0)與函數(shù)N的圖象組成的圖形記為W,若圖形W與線段AB恰有2個公共點,直接寫出a的取值范圍.組卷:1196引用:2難度:0.2


