2021-2022學年江蘇省蘇州市吳江高級中學高二(下)期中數學試卷
發布:2024/11/11 2:0:2
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.若函數f(x)的導函數為f′(x),且滿足f(x)=2f′(1)lnx+2x,則f′(1)=( )
A.0 B.-1 C.-2 D.2 組卷:844引用:8難度:0.8 -
2.已知隨機變量X~B(6,p),Y~N(μ,σ2),且P(Y≥2)=
,E(X)=E(Y),則p=( )12A. 12B. 13C. 14D. 16組卷:320引用:8難度:0.8 -
3.若(1+mx2)(1+x)4的展開式中x3的系數為12,則實數m=( )
A.1 B.2 C.3 D.4 組卷:258引用:2難度:0.8 -
4.函數f(x)=
的圖象大致為( )ex-e-xx2A. 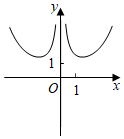
B. 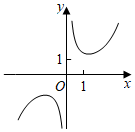
C. 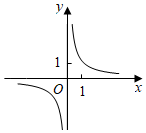
D. 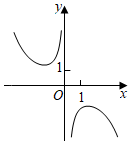 組卷:1946引用:128難度:0.9
組卷:1946引用:128難度:0.9 -
5.疫苗是為預防、控制傳染病的發生、流行,用于人體預防接種的預防性生物制品,其前期研發過程中,一般都會進行動物保護測試,為了考察某種疫苗預防效果,在進行動物試驗時,得到如下統計數據:
附表及公式:未發病 發病 總計 未注射疫苗 20 注射疫苗 30 總計 50 50 100 ,n=a+b+c+d.K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)
現從試驗動物中任取一只,取得“注射疫苗”的概率為P(K2≥k0) 0.05 0.01 0.005 0.001 k0 3.841 6.635 7.879 10.828 ,則下列判斷錯誤的是( )25A.注射疫苗發病的動物數為10 B.從該試驗未注射疫苗的動物中任取一只,發病的概率為 23C.能在犯錯概率不超過0.001的前提下,認為疫苗有效 D.該疫苗的有效率為75% 組卷:363引用:2難度:0.6 -
6.某一電子集成塊有三個元件a,b,c并聯構成,三個元件是否有故障相互獨立.已知至少1個元件正常工作,該集成塊就能正常運行.若每個元件能.正常工作的概率均為
,則在該集成塊能夠正常工作的情況下,有且僅有一個元件出現故障的概率為( )45A. 1231B. 48125C. 1625D. 16125組卷:338引用:5難度:0.7 -
7.已知f'(x)是函數f(x)的導函數,且對任意的實數x都有f'(x)=ex(2x+1)+f(x),f(0)=-2,則不等式f(x)<4ex的解集為( )
A.(-2,3) B.(-3,2) C.(-∞,-3)∪(2,+∞) D.(-∞,-2)∪(3,+∞) 組卷:527引用:4難度:0.7
四、解答題:本題共6小題,共70分.解答時應寫出文字說明、證明過程或演算步驟.
-
21.已知函數
,a,b∈R,且a>0.f(x)=aex+b?exx
(1)若函數f(x)在處取得極值x=12,求函數f(x)的解析式;4e
(2)在(1)的條件下,令,求g(x)的單調區間;g(x)=f(x)-2lnx-1x組卷:101引用:3難度:0.5 -
22.已知函數
.f(x)=alnx+2x+a
(1)若f(x)在[1,2]上單調遞減,求a的取值范圍;
(2)若f(x)有兩個零點x1,x2,求a的取值范圍;
(3)證明:當a=1時,若對于任意正實數x1,x2,且x1<x2,若f(x1)=f(x2),則x1+x2>4.組卷:158引用:2難度:0.3


