2017-2018學年上海市浦東新區華東師大二附中高三（上）開學數學試卷

一、填空題（本大題滿分54分）本大題共有12題，1-6題每題4分，7-12題每題5分

• 1．集合A={1，2}，B={2，3}，則A∪B=

  ．
  組卷：164引用：20難度：0.9

  解析

• 2．已知i是虛數單位，復數z滿足

  z

  ?

  （

  1

  +

  3

  i

  ）

  =

  1

  ，則|z|=

  ．
  組卷：391引用：7難度：0.9

  解析

• 3．函數f（x）=

  2 cosx	sinx
  sinx	2 cosx

  的最小正周期為

  ．
  組卷：41引用：3難度：0.9

  解析

• 4．已知單位向量

  i

  ,

  j

  滿足

  （

  2

  j

  -

  i

  ）

  ⊥

  i

  ，則

  i

  ,

  j

  的夾角為

  ．
  組卷：18引用：1難度：0.9

  解析

• 5．將8個三好生名額分配給甲、乙、丙、丁4個班級，每班至少1個名額，則甲班恰好分到2個名額的概率為

  ．
  組卷：154引用：1難度：0.5

  解析

• 6．已知y=f^-1（x）是函數f（x）=arcsin（1-x）的反函數，則f^-1（x）=

  ．
  組卷：28引用：3難度：0.7

  解析

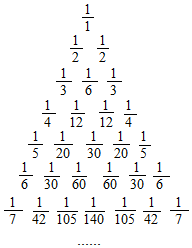• 7．將楊輝三角中的每一個數

  C

  r

  n

  都換成

  1

  （

  n

  +

  1

  ）

  C

  r

  n

  ，就得到一個如圖所示的分數三角形，成為萊布尼茨三角形．令

  a

  n

  =

  1

  3

  +

  1

  12

  +

  1

  30

  +

  1

  60

  +

  …

  +

  1

  n

  C

  2

  n

  -

  1

  +

  1

  （

  n

  +

  1

  ）

  C

  n

  2

  ，則

  lim

  n

  →∞

  a

  n

  =

  ．
  組卷：23引用：1難度：0.5

  解析

三、解答題（本大題滿分78分）本大題共有5題

• 20．已知函數f（x）=log_a（x+1）（a＞1），函數g（x）的圖象與函數

  y

  =

  3

  2

  +

  a

  x

  -

  3

  4

  （a＞1）的圖象關于直線y=x對稱．
  （1）求函數g（x）的解析式；
  （2）若函數g（x）在區間

  [

  m

  ,

  n

  ]

  （

  m

  ＞

  3

  2

  ）

  上的值域為[log_a（p+3m），log_a（p+3n）]，求實數p的取值范圍；
  （3）設函數F（x）=a^{f（x）-g（x）}（a＞1），試用列舉法表示集合M={x|F（x）∈Z}．
  組卷：91引用：4難度：0.3

  解析

• 21．已知集合S=

  {

  k

  |

  1

  ≤

  k

  ≤

  3

  n

  -

  1

  2

  ，

  k

  ∈

  N

  *

  }

  （n≥2，且n∈N^*）．若存在非空集合S₁，S₂，…，S_n，使得S=S₁∪S₂∪…∪S_n，且S_i∩S_j=?（1≤i,j≤n,i≠j），并?x,y∈S_i（i=1，2，…，n），x＞y,都有x-y?S_i，則稱集合S具有性質P，S_i（i=1，2，…，n）稱為集合S的P子集．
  （Ⅰ）當n=2時，試說明集合S具有性質P，并寫出相應的P子集S₁，S₂；
  （Ⅱ）若集合S具有性質P，集合T是集合S的一個P子集，設T′={s+3ⁿ|s∈T}，求證：?x,y∈T∪T′，x＞y,都有x-y?T∪T′；
  （Ⅲ）求證：對任意正整數n≥2，集合S具有性質P．
  組卷：339引用：2難度：0.1

  解析