2022-2023學(xué)年浙江省金華市部分學(xué)校九年級(jí)（上）期末數(shù)學(xué)試卷

一、選擇題（本題有10小題，每小題3分，共30分）

• 1．已知2：x=3：y,則x：y等于（　　）

  A．2

  B．3

  C．2：3

  D．3：2
  組卷：111引用：1難度：0.8

  解析

• 2．若y=（m-2）

  x

  m

  2

  -

  2

  是二次函數(shù)，則m的值為（　　）

  A．±2

  B．2

  C．-2

  D．± 3
  組卷：576引用：5難度：0.9

  解析

• 3．已知點(diǎn)P到圓心O的距離為3cm,點(diǎn)P在⊙O內(nèi)，則⊙O的半徑R的取值范圍是（　　）

  A．R＞3

  B．R＜3

  C．0＜R＜3

  D．R≥3
  組卷：210引用：2難度：0.8

  解析

• 4．“若a是實(shí)數(shù)，則a²＜0”這一事件是（　　）

  A．必然事件

  B．不可能事件

  C．不確定事件

  D．隨機(jī)事件
  組卷：274引用：2難度：0.7

  解析

• 5．已知（1，y₁），（3，y₂）是函數(shù)y=-2x²+6x+c圖象上的點(diǎn)，則y₁，y₂的大小關(guān)系是（　　）

  A．y1＞y2

  B．y1＜y2

  C．y1=y2

  D．無(wú)法確定
  組卷：127引用：1難度：0.5

  解析

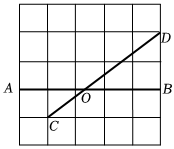• 6．如圖，在正方形方格紙中，每個(gè)小的四邊形都是相同的正方形，點(diǎn)A、B、C、D都在格點(diǎn)處，AB與CD相交于點(diǎn)O，則∠BOD的正弦值是（　　）

  A． 4 5

  B． 3 4

  C． 4 3

  D． 3 5
  組卷：255引用：1難度：0.6

  解析

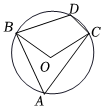• 7．如圖，⊙O中，點(diǎn)D、A分別在劣弧BC和優(yōu)弧BC上，∠BOC=100°，則∠BDC=（　　）

  A．50°

  B．80°

  C．125°

  D．130°
  組卷：280引用：1難度：0.8

  解析

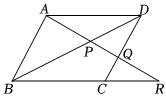• 8．如圖?ABCD中，Q是CD上的點(diǎn)，AQ交BD于點(diǎn)P，交BC的延長(zhǎng)線于點(diǎn)R，若DQ：CQ=4：1，則AP：PR=（　　）

  A．5：4

  B．4：5

  C．3：4

  D．5：8
  組卷：547引用：1難度：0.5

  解析

三、解答題（本題有8小題，共66分，各小題都必須寫(xiě)出解答過(guò)程）

• 23．閱讀理解：
  （1）【學(xué)習(xí)心得】
  小趙同學(xué)在學(xué)習(xí)完“圓”這一章內(nèi)容后，感覺(jué)到一些幾何問(wèn)題，如果添加輔助圓，運(yùn)用圓的知識(shí)解決，可以使問(wèn)題變得非常容易．我們把這個(gè)過(guò)程稱為“化隱圓為顯圓”．這類題目主要是兩種類型．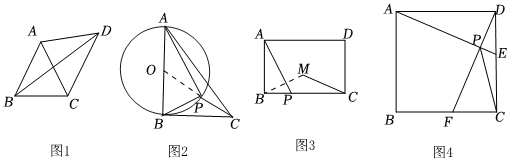
  
  ①類型一，“定點(diǎn)+定長(zhǎng)”：如圖1，在△ABC中，AB=AC，∠BAC=44°，D是△ABC外一點(diǎn)，且AD=AC，求∠BDC的度數(shù)．
  解：若以點(diǎn)A（定點(diǎn)）為圓心，AB（定長(zhǎng)）為半徑作輔助圓⊙A，（請(qǐng)你在圖1上畫(huà)圓）則點(diǎn)C、D必在⊙A上，∠BAC是⊙A的圓心角，而∠BDC是圓周角，從而可容易得到∠BDC=

  °．
  ②類型二，“定角+定弦”：如圖，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC內(nèi)部的一個(gè)動(dòng)點(diǎn)，且滿足∠PAB=∠PBC，求線段CP長(zhǎng)的最小值．
  解：∵∠ABC=90°，
  ∴∠ABP+∠PBC=90°，∵∠PAB=∠PBC，∴∠BAP+∠ABP=90°，
  ∴∠APB=

  ，（定角）
  ∴點(diǎn)P在以AB（定弦）為直徑的⊙O上，請(qǐng)完成后面的過(guò)程．
  （2）【問(wèn)題解決】
  如圖3，在矩形ABCD中，已知AB=3，BC=4，點(diǎn)P是BC邊上一動(dòng)點(diǎn)（點(diǎn)P不與B，C重合），連接AP，作點(diǎn)B關(guān)于直線AP的對(duì)稱點(diǎn)M，則線段MC的最小值為

  ．
  （3）【問(wèn)題拓展】
  如圖4，在正方形ABCD中，AD=4，動(dòng)點(diǎn)E，F(xiàn)分別在邊DC，CB上移動(dòng)，且滿足DE=CF．連接AE和DF，交于點(diǎn)P．
  ①請(qǐng)你寫(xiě)出AE與DF的數(shù)量關(guān)系和位置關(guān)系，并說(shuō)明理由；
  ②點(diǎn)E從點(diǎn)D開(kāi)始運(yùn)動(dòng)到點(diǎn)C時(shí)，點(diǎn)P也隨之運(yùn)動(dòng)，請(qǐng)求出點(diǎn)P的運(yùn)動(dòng)路徑長(zhǎng)．
  組卷：2832引用：7難度：0.3

  解析

• 24．如圖1，已知點(diǎn)A的坐標(biāo)是（-1，0），點(diǎn)B的坐標(biāo)是（9，0），以AB為直徑作⊙O′，交y軸的正半軸于點(diǎn)C，連接AC、BC，過(guò)A、B、C三點(diǎn)作拋物線．
  
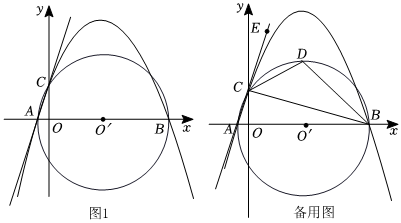
  （1）求點(diǎn)C的坐標(biāo)及拋物線的解析式；
  （2）如圖2，點(diǎn)E是AC延長(zhǎng)線上一點(diǎn)，∠BCE的平分線CD交⊙O′于點(diǎn)D，求點(diǎn)D的坐標(biāo)；并直接寫(xiě)出直線BC、直線BD的解析式；
  （3）在（2）的條件下，拋物線上是否存在點(diǎn)P，使得∠PDB=∠CBD，若存在，請(qǐng)求出點(diǎn)P的橫坐標(biāo)，若不存在，請(qǐng)說(shuō)明理由．
  組卷：339引用：1難度：0.3

  解析