2022-2023學(xué)年北京市海淀區(qū)清華附中七年級（下）期中數(shù)學(xué)試卷

一、選擇題（本題共24分，每小題3分）第1-8題均有四個選項，符合題意的選項只有一個

• 1．下列各式中，正確的是（　　）

  A． 16 =±4

  B．± 16 =4

  C． 3 - 27 =-3

  D． （ - 4 ） 2 =-4
  組卷：4135引用：221難度：0.9

  解析

• 2．若m＞-1，則下列各式中錯誤的是（　　）

  A．4m＞-4

  B．-5m＜-5

  C．m+1＞0

  D．1-m＜2
  組卷：234引用：2難度：0.8

  解析

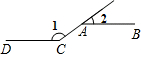• 3．如圖所示，AB∥CD，若∠1=144°，則∠2的度數(shù)是（　　）

  A．30°

  B．32°

  C．34°

  D．36°
  組卷：554引用：6難度：0.7

  解析

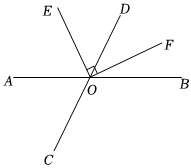• 4．如圖，直線AB與直線CD相交于點O，OE⊥OF，且OA平分∠COE，若∠DOE=50°，則∠BOF的度數(shù)為（　　）

  A．20°

  B．25°

  C．30°

  D．35°
  組卷：137引用：8難度：0.7

  解析

• 5．下列圖形中，不能通過其中一個四邊形平移得到的是（　　）

  A．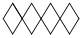

  B．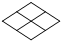

  C．

  D．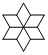
  組卷：901引用：38難度：0.9

  解析

• 6．如圖，將5個大小相同的正方形置于平面直角坐標系中，若頂點M、N的坐標分別為（3，9）、（12，9），則頂點A的坐標為（　　）

  A．（15，3）

  B．（16，4）

  C．（15，4）

  D．（12，3）
  組卷：720引用：6難度：0.6

  解析

• 7．已知關(guān)于x,y的方程組

  x + 2 y - 6 = 0

  x - 2 y + mx + 5 = 0

  ，若方程組的解中x恰為整數(shù)，m也為整數(shù)，則m的值為（　　）

  A．-1

  B．1

  C．-1或3

  D．-1或-3
  組卷：1668引用：6難度：0.7

  解析

二、填空題（本題共24分，每小題3分）

• 8．若一個二元一次方程組的解是

  x = 2

  y = 1 .

  請寫出一個符合此要求的二元一次方程組

   

  ．
  組卷：390引用：3難度：0.7

  解析

• 9．小亮解方程組

  2 x + y =●

  2 x - y = 10

  的解為

  x = 4

  y =▲

  ，由于不小心，滴上了兩滴墨水，剛好遮住了兩個數(shù)●和▲，請你幫他找回▲，這個數(shù)▲=

  ．
  組卷：494引用：1難度：0.5

  解析

三、解答題（本題共52分，第17題，4分；第18題，每小題4分：第19-20題，每小5分：第21-25題，每小題4分）解答應(yīng)寫出文字說明、演算步驟或證明過程

• 28．已知x+y+7z=0，x-y-3z=0（xyz≠0），則

  2

  x

  +

  y

  +

  z

  2

  x

  -

  y

  +

  z

  =

  ．
  組卷：2119引用：5難度：0.6

  解析

• 29．在平面直角坐標系xOy中，對于與原點不重合的兩個點P（a,b）和Q（c,d），關(guān)于x,y的方程ax+by=1稱
  為點P的“照耀方程”．若

  x = c

  y = d

  是方程ax+by=1的解，則稱點P“照耀”了點Q．
  例如，點P（5，7）的“照耀方程”是5x+7y=1，且

  x = 3

  y = - 2

  是該方程的解，則點P（5，7）“照耀”了點Q（3，-2）．
  （1）下列點中被點A（3，-2）“照耀”的點為

  ；
  B₁（-1，1），B₂（4，6），B₃（5，7）
  （2）若點C（p,q）同時被點D（5，-9）和點E（-3，7）“照耀”，請求出p,q；
  （3）若n個不同的點P₁，P₂，…，P_n，每個點都“照耀”了其后所有的點，
  如P₁“照耀”了P₂，P₃，…，P_n，
  P₂“照耀”了P₃，P₄，…，P_n，
  …
  P_n-1“照耀”了P_n，
  請寫出n的最大值，并說明理由．
  組卷：286引用：2難度：0.5

  解析