2022-2023學年浙江省杭州十四中高一（下）期中數學試卷

一．選擇題：本大題共8小題，每小題5分，共40分．每小題列出的四個選項中只有一個是符合題目要求的，不選、多選、錯選均不得分.

• 1．復數

  z

  =

  3

  +

  i

  1

  +

  i

  在復平面上對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：60引用：4難度：0.8

  解析

• 2．“a＞b”是“lga＞lgb”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：153引用：8難度：0.8

  解析

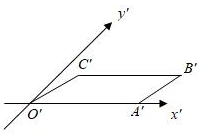• 3．如圖，平行四邊形O'A'B'C'是水平放置的一個平面圖形的直觀圖，其中O'A'=5，O'C'=2，∠A'O'C'=30°，則原圖形的面積是（　　）

  A．4

  B． 4 2

  C． 10 2

  D．6
  組卷：336引用：4難度：0.9

  解析

• 4．已知l是直線，α、β是兩個不同平面，下列命題中的真命題是（　　）

  A．若l∥α，l∥β，則α∥β	B．若α⊥β，l∥α，則l⊥β
  C．若l⊥α，l∥β，則α⊥β	D．若l∥α，α∥β，則l∥β
  組卷：273引用：13難度：0.9

  解析

• 5．在△ABC中，點D在邊BC的延長線上，且

  BC

  =

  3

  CD

  ．若

  AO

  =

  x

  AB

  +

  （

  1

  -

  x

  ）

  AC

  ，-

  1

  3

  ＜x＜0，則點O在（　　）

  A．線段BC上

  B．線段CD上

  C．線段AC上

  D．線段AD上
  組卷：159引用：5難度：0.6

  解析

• 6．如表為某港口在某季節中每天水深與時刻的關系：
  

  時刻	0：00	3：00	6：00	9：00	12：00	15：00	18：00	21：00	24：00
  水深（單位：m）	5	7	5	3	5	7	5	3	5

  若該港口水深y（單位：m）和時刻t（0≤t≤24）的關系可用函數y=Asin（ωt+φ）+h來近似描述，則該港口在11：00的水深（單位：m）為（　　）

  A．4

  B．5 - 2

  C．5- 3

  D．3- 3
  組卷：35引用：2難度：0.6

  解析

• 7．在直三棱柱ABC-A₁B₁C₁中，

  AB

  =

  4

  ，

  BC

  =

  AC

  =

  2

  2

  ，

  A

  A

  1

  =

  1

  ，點M，N分別是A₁B₁，A₁C₁的中點，則直線BM與CN所成角的余弦值為（　　）

  A． 15 5

  B． 10 5

  C． 5 3

  D． 6 3
  組卷：277引用：4難度：0.7

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟.

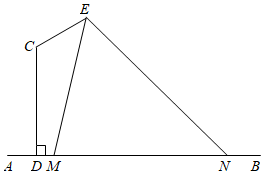• 21．我校在一條水泥路邊安裝路燈，其中燈桿的設計如圖所示，AB為底面，CD、CE為路燈的燈桿，CD⊥AB，且

  ∠

  DCE

  =

  2

  3

  π

  ，在E處安裝路燈，且路燈的照明張角為

  ∠

  MEN

  =

  π

  3

  ，已知CD=5米，CE=3米．
  （1）當M與D重合時，求路燈在路面的照明寬度MN；
  （2）求此路燈在路面上的照明寬度MN的最小值．
  組卷：196引用：3難度：0.6

  解析

• 22．若在定義域內存在實數x₀，使得f（x₀+1）=f（x₀）+f（1）成立，則稱函數有“飄移點”x₀．
  （1）函數

  f

  （

  x

  ）

  =

  1

  x

  是否有“飄移點”？請說明理由；
  （2）證明函數f（x）=x²+2^x在（0，1）上有“飄移點”；
  （3）若函數

  f

  （

  x

  ）

  =

  lg

  （

  a

  x

  2

  +

  1

  ）

  在（0，1）上有“飄移點”，求實數a的取值范圍．
  組卷：54引用：2難度：0.5

  解析