2022-2023學年山東省臨沂市莒南縣九年級（上）期中數學試卷

一、單選題（每題3分，共36分）

• 1．下列圖形中，是中心對稱圖形的是（　　）

  A．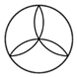

  B．

  C．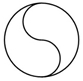

  D．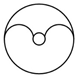
  組卷：955引用：57難度：0.9

  解析

• 2．下列關于拋物線y=-（x+2）²+3的性質說法正確的是（　　）

  A．開口向上	B．頂點坐標是（2，3）
  C．對稱軸是直線x=-2	D．當-5＜x≤0時，-6＜y≤-1
  組卷：193引用：2難度：0.7

  解析

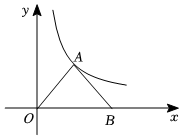• 3．如圖，點A在反比例函數y=

  a

  x

  第一象限內的圖象上，點B在x軸的正半軸上，OA=AB，△AOB的面積為2，則a的值為（　　）

  A． - 1 2

  B． 1 2

  C．2

  D．1
  組卷：332引用：6難度：0.7

  解析

• 4．關于函數

  y

  =

  -

  1

  x

  的圖象，下列說法錯誤的是（　　）

  A．該函數圖象是雙曲線

  B．經過點（1，1）

  C．在第二象限內，y隨x的增大而增大

  D．是中心對稱圖形，且對稱中心是坐標原點
  組卷：114引用：2難度：0.5

  解析

• 5．點A（-2，y₁），B（0，y₂），C（1，y₃）為二次函數y=x²-2x+1的圖象上的三點，則y₁，y₂，y₃的大小關系是（　　）

  A．y1＜y2＜y3

  B．y3＜y2＜y1

  C．y3＜y1＜y2

  D．y1＜y3＜y2
  組卷：1029引用：12難度：0.6

  解析

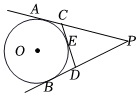• 6．如圖，PA，PB切⊙O于點A，B，PA=20，CD切⊙O于點E，交PA，PB于C，D兩點，則△PCD的周長是（　　）

  A．20

  B．36

  C．40

  D．44
  組卷：110引用：5難度：0.7

  解析

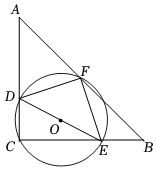• 7．如圖，在△ABC中，∠C=90°，AC=BC=6，點D，E分別在AC和BC上，CD=2，若以DE為直徑的⊙O交AB的中點F，可知⊙O的直徑是（　　）

  A． 2 3

  B．2

  C． 2 5

  D．5
  組卷：100引用：4難度：0.5

  解析

三、解答題（共68分）

• 22．已知，AB是⊙O的直徑，AB=16，點C在⊙O的半徑OA上運動，PC⊥AB，垂足為C，PC=10，PT為⊙O的切線，切點為T．
  （1）如圖（1），當C點運動到O點時，求PT的長；
  （2）如圖（2），當C點運動到A點時，連接PO、BT，求證：PO∥BT；
  （3）如圖（3），設PT=y,AC=x,求y與x的解析式并求出y的最小值．
  
  組卷：174引用：2難度：0.2

  解析

• 23．若任意兩個正數的和為定值，則它們的乘積會如何變化呢？會不會存在最大值？
  特例研究：若兩個正數的和是1，那么這兩個正數可以是：

  1

  2

  和

  1

  2

  ，

  1

  4

  和

  3

  4

  ，

  1

  5

  和

  4

  5

  ，…
  由于這樣的正數有很多，我們不妨設其中一個正數是x,另外一個正數為y,那么x+y=1，則y=1-x,所以z=xy=x（1-x）=-x²+x,0＜x＜1，可以看出兩數的乘積z是x的二次函數，乘積的最大值轉化為求關于x的二次函數的最值問題．
  方法遷移：
  （1）若兩個正數x和y的和是6，其中一個正數為x（0＜x＜6），這兩個正數的乘積為z,寫出z與x的函數關系式，并畫出函數圖象．
  
  （2）在（1）的條件下，z的最大值為：

  ，并寫出此時函數圖象的至少一個性質．
  （3）問題解決：
  由以上題目可知若任意兩個正數的和是一個固定的數，那么這兩個正數的乘積存在最大值，即對于正數x,y,若x+y是定值，則xy存在最大值．
  類比應用：
  利用上面所得到的結論，完成填空：
  ①已知函數y₁=2x-2（x＞1）與函數y₂=-2x+8（x＜4），則當x=

  時，y₁?y₂取得最大值為

  ；
  ②已知函數y₁=2x-2+m（x≥1），m為正定值，函數y₂=-2x+8（x＜4），則當x為何值時，y₁?y₂取得最大值，最大值是多少？
  組卷：84引用：2難度：0.1

  解析