2021-2022學(xué)年河北省石家莊市高二（下）期末數(shù)學(xué)試卷

一、單項(xiàng)選擇題（本題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.）

• 1．已知函數(shù)f（x）=

  x

  ，f′（16）=（　　）

  A． 1 8

  B． 1 4

  C． 1 2

  D．2
  組卷：104引用：6難度：0.8

  解析

• 2．在下列兩個(gè)分類變量X，Y的樣本頻數(shù)列聯(lián)表中，可以判斷X、Y之間有無(wú)關(guān)系的是（　　）
  

  	y1	y	總計(jì)
  x1	a	b	a+b
  x2	c	d	c+d
  總計(jì)	a+c	b+d	a+b+c+d

  A．| a a + b - b c + d |

  B．| c a + b - d c + d |

  C．| b a + b - c c + d |

  D．| a a + b - c c + d |
  組卷：50引用：1難度：0.7

  解析

• 3．使函數(shù)f（x）=x+

  2

  cosx在[0，

  π

  2

  ]上取最大值的x為（　　）

  A．0

  B． π 4

  C． π 3

  D． π 2
  組卷：67引用：3難度：0.7

  解析

• 4．已知三個(gè)正態(tài)分布密度函數(shù)φ_i（x）=

  1

  2

  π

  σ

  i

  e

  -

  （

  x

  -

  μ

  i

  ）

  2

  2

  σ

  2

  i

  （x∈R，i=1，2，3）（其中，e為自然對(duì)數(shù)的底數(shù)）的圖象如圖所示，則下列結(jié)論正確的是（　　）

  A．σ1=σ2＞σ3

  B．μ1＞μ3

  C．σ2＜σ3

  D．μ1=u2
  組卷：49引用：1難度：0.7

  解析

• 5．函數(shù)f（x）=

  1

  x

  -

  lnx

  -

  1

  的圖象大致是（　　）

  A．

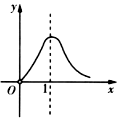
  B．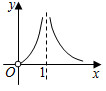

  C．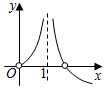

  D．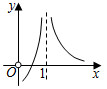
  組卷：323引用：24難度：0.9

  解析

• 6．對(duì)具有線性相關(guān)關(guān)系的變量x,y有一組觀測(cè)數(shù)據(jù)（x_i，y_i）（i=1，2…，8），其回歸直線方程是

  ?

  y

  =

  1

  3

  x+

  ?

  a

  ，且x₁+x₂+…+x₈=2（y₁+y₂+…+y₈）=6，則當(dāng)x=-

  3

  4

  時(shí)，y的估計(jì)值為（　　）

  A．- 1 8

  B． 1 8

  C．- 1 4

  D． 1 4
  組卷：22引用：1難度：0.8

  解析

• 7．七巧板又稱七巧圖、智慧板，是中國(guó)古代勞動(dòng)人民的發(fā)明，其歷史至少可以追溯到公元前一世紀(jì)，到了明代基本定型，于明、清兩代在民間廣泛流傳．某同學(xué)用邊長(zhǎng)4寸的正方形木板制作了一套七巧板，如圖所示，包括5個(gè)等腰直角三角形，1個(gè)正方形和1個(gè)平行四邊形．現(xiàn)他從5個(gè)三角形中隨意取出兩個(gè)，則這兩個(gè)三角形的面積之和不小于另外三個(gè)三角形面積之和的概率是（　　）

  A． 1 5

  B． 3 10

  C． 2 5

  D． 1 2
  組卷：43引用：4難度：0.7

  解析

四、解答題（本題共6小題，共70分.解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.）

• 21．已知函數(shù)f（x）=e^x-x-a,對(duì)于?x∈R，f（x）≥0恒成立．
  （1）求實(shí)數(shù)a的取值范圍；
  （2）證明：當(dāng)

  x

  ∈

  [

  0

  ，

  π

  4

  ]

  時(shí)，cosx+tanx≤e^x．
  組卷：266引用：6難度：0.4

  解析

• 22．已知函數(shù)f（x）=x-lnx+a（a∈R）．
  （Ⅰ）求函數(shù)f（x）的極值；
  （Ⅱ）設(shè)函數(shù)f（x）的圖象與直線y=t交于M（x₁，t），B（x₂，t）兩點(diǎn)，且x₁＜x₂，求證：函數(shù)f（x）在x=

  x

  1

  +

  x

  2

  2

  處的切線斜率大于0．
  組卷：27引用：1難度：0.6

  解析