2022-2023學年浙江省金華五中八年級（上）期初數學試卷

一、選擇題（本題有10小題，每小題3分，共30分）

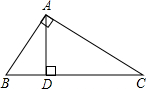• 1．如圖，∠BAC=90°，AD⊥BC，則圖中互余的角有（　　）

  A．2對

  B．3對

  C．4對

  D．5對
  組卷：1218引用：32難度：0.9

  解析

• 2．已知2x-3y=3，3y-4z=5，x+2z=8，則代數式3x²-12z²的值是（　　）

  A．32

  B．64

  C．96

  D．128
  組卷：307引用：1難度：0.6

  解析

• 3．下列命題：（1）無限循環小數是無理數；（2）絕對值等于它本身的數是非負數；（3）垂直于同一直線的兩條直線互相平行；（4）有兩邊和其中一邊的對角對應相等的兩個三角形全等；（5）面積相等的兩個三角形全等，是假命題的有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：72引用：1難度：0.6

  解析

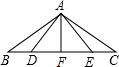• 4．如圖所示，在△ABC中，AB=AC，∠B=∠C，D、E在BC上，BD=CE，AF⊥BC于F，則圖中全等三角形的對數為（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：30引用：4難度：0.7

  解析

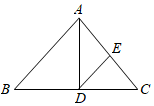• 5．如圖，在△ABC中，∠B=46°，∠C=52°，AD平分∠BAC，交BC于點D，DE∥AB，交AC于點E，則∠ADE=（　　）

  A．45°

  B．41°

  C．40°

  D．50°
  組卷：133引用：2難度：0.7

  解析

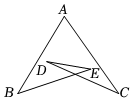• 6．如圖，已知∠A=60°，∠B=40°，∠C=30°，則∠D+∠E等于（　　）

  A．30°

  B．40°

  C．50°

  D．60°
  組卷：3038引用：20難度：0.6

  解析

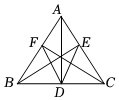• 7．如圖，在△ABC中，AB=AC，AD是△ABC的角平分線，BE⊥AC，CF⊥AB，垂足分別為E，F．則下列四個結論：①AD上任意一點到點C，B的距離相等；②AD上任意一點到邊AB，AC的距離相等；③BD=CD，AD⊥BC；④∠BDE=∠CDF；⑤BC=AD．其中，正確的個數為（　　）

  A．2個

  B．3個

  C．4個

  D．5個
  組卷：36引用：1難度：0.6

  解析

• 8．在△ABC中，AC=6，中線AD=10，則AB邊的取值范圍是（　　）

  A．16＜AB＜22

  B．14＜AB＜26

  C．16＜AB＜26

  D．14＜AB＜22
  組卷：1232引用：8難度：0.6

  解析

三、解答題（本題有8個小題，共66分）

• 23．【問題背景】
  如圖1，在四邊形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，點E、F分別是邊BC、CD上的點，且∠EAF=60°，試探究圖中線段BE、EF、FD之間的數量關系．
  小王同學探究此問題的方法是：延長FD到點G，使GD=BE，連結AG，先證明△ABE≌△ADG，再證明△AEF≌△AGF，可得出結論，他的結論應是

  ．
  【探索延伸】
  如圖2，若在四邊形ABCD中，AB=AD，∠B+∠D=180°，點E、F分別是邊BC、CD上的點，且∠EAF=

  1

  2

  ∠BAD，上述結論是否仍然成立，并說明理由．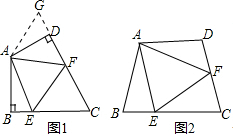
  
  組卷：316引用：3難度：0.2

  解析

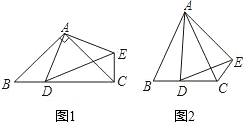• 24．在△ABC中，AB=AC，點D是直線BC上一點（不與B、C重合），以AD為一邊在AD的右側作△ADE，使AD=AE，∠DAE=∠BAC，連接CE．
  （1）如圖1，當點D在線段BC上，如果∠BAC=90°，則∠BCE=

  度；
  （2）設∠BAC=α，∠BCE=β．
  ①如圖2，當點D在線段BC上移動，則α，β之間有怎樣的數量關系？請說明理由；
  ②當點D在直線BC上移動，則α，β之間有怎樣的數量關系？請直接寫出你的結論．
  組卷：6428引用：109難度：0.1

  解析