2023年吉林省松原市前郭縣西部學區中考數學一模試卷

一、選擇題（每小題2分，共12分）

• 1．下列計算結果為5的是（　　）

  A．-（+5）

  B．+（-5）

  C．-（-5）

  D．-|-5|
  組卷：1240引用：22難度：0.7

  解析

• 2．2、5、m是某三角形三邊的長，則

  （

  m

  -

  3

  ）

  2

  +

  （

  m

  -

  7

  ）

  2

  等于（　　）

  A．2m-10

  B．10-2m

  C．10

  D．4
  組卷：3953引用：38難度：0.7

  解析

• 3．下列四幅圖片上呈現的是垃圾類型及標識圖案，其中標識圖案是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：869引用：13難度：0.8

  解析

• 4．不等式3x+1＜2x的解集在數軸上表示正確的是（　　）

  A．

  B．

  C．

  D．
  組卷：789引用：12難度：0.8

  解析

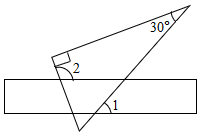• 5．將含30°角的一個直角三角板和一把直尺如圖放置，若∠1=50°，則∠2等于（　　）

  A．80°

  B．100°

  C．110°

  D．120°
  組卷：882引用：16難度：0.7

  解析

• 6．如圖，圓柱的底面直徑為AB，高為AC，一只螞蟻在C處，沿圓柱的側面爬到B處，現將圓柱側面沿AC“剪開”，在側面展開圖上畫出螞蟻爬行的最近路線，正確的是（　　）

  A．

  B．

  C．

  D．
  組卷：2944引用：26難度：0.5

  解析

二、填空題（每小題3分，共24分）

• 7．分解因式：m³-4m=

  ．
  組卷：1685引用：209難度：0.7

  解析

• 8．為了解某校學生對湖南省“強省會戰略”的知曉情況，從該校全體1000名學生中，隨機抽取了100名學生進行調查．結果顯示有95名學生知曉．由此，估計該校全體學生中知曉湖南省“強省會戰略”的學生有

  名．
  組卷：679引用：4難度：0.6

  解析

六、解答題（每小題10分，共20分）

• 25．問題背景：
  一次數學綜合實踐活動課上，小慧發現并證明了關于三角形角平分線的一個結論．如圖1，已知AD是△ABC的角平分線，可證

  AB

  AC

  =

  BD

  CD

  ．小慧的證明思路是：如圖2，過點C作CE∥AB，交AD的延長線于點E，構造相似三角形來證明

  AB

  AC

  =

  BD

  CD

  ．
  嘗試證明：
  （1）請參照小慧提供的思路，利用圖2證明：

  AB

  AC

  =

  BD

  CD

  ；
  應用拓展：
  （2）如圖3，在Rt△ABC中，∠BAC=90°，D是邊BC上一點．連接AD，將△ACD沿AD所在直線折疊，點C恰好落在邊AB上的E點處．
  ①若AC=1，AB=2，求DE的長；
  ②若BC=m,∠AED=α，求DE的長（用含m,α的式子表示）．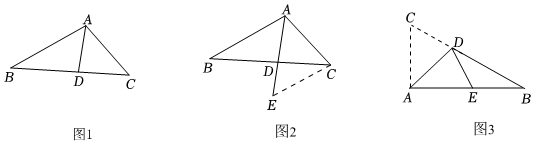
  
  組卷：2536引用：17難度：0.4

  解析

• 26．已知二次函數y=-x²+6x-5．
  （1）求二次函數圖象的頂點坐標；
  （2）當1≤x≤4時，函數的最大值和最小值分別為多少？
  （3）當t≤x≤t+3時，函數的最大值為m,最小值為n,若m-n=3，求t的值．
  組卷：4850引用：12難度：0.6

  解析