當前位置：試卷中心 > 試卷詳情

2022-2023學年山東省淄博市張店區八年級（下）期末數學試卷（五四學制）

發布：2024/7/7 8:0:9

一、選擇題（本題共10小題，每小題4分，共40分．在每小題所給出的四個選項中，只有一個是正確的，請把正確的選項填涂在答題紙的相應位置上）

1．代數式
x
-
3
在實數范圍內有意義，則x的取值范圍是（　　）
A．x≥3 B．x＞3 C．x≤3 D．x＜3
組卷：781引用：10難度：0.8
解析
2．若
a
b
=
2
3
，則
a
+
b
b
的值為（　　）
A．
2
5
B．
5
2
C．
3
5
D．
5
3
組卷：1046引用：11難度：0.7
解析
3．下列計算中，正確的是（　　）
A．
2
+
2
=
2
2
B．
6
×
3
=
3
2
C．
（
-
2
）
2
=±
2
D．
15
÷
3
=
5
組卷：114引用：4難度：0.7
解析
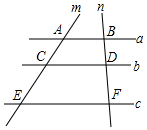4．如圖，直線a∥b∥c,直線a,b,c分別交直線m,n于點A，C，E，B，D，F，若AC=2，CE=4，BD=1，則DF=（　　）
A．2 B．3 C．
3
2
D．
7
2
組卷：285引用：1難度：0.7
解析
5．一元二次方程x²-6x-1=0配方后可變形為（　　）
A．（x+3）²=10 B．（x+3）²=8 C．（x-3）²=10 D．（x-3）²=8
組卷：1582引用：27難度：0.8
解析
6．菱形，矩形，正方形都具有的性質是（　　）
A．四條邊相等，四個角相等
B．對角線相等
C．對角線互相垂直
D．對角線互相平分
組卷：6302引用：59難度：0.9
解析
7．如圖，△ABC與△DEF是位似圖形，位似中心為O，OA=2，AD=3，△ABC的面積為4，則△DEF的面積為（　　）
A．6 B．9 C．10 D．25
組卷：208引用：3難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本題共8小題，共計90分，請把解答過程寫在答題紙上）

22．【閱讀理解】
配方法是中學數學的重要方法，用配方法可求最大（小）值．對于任意正實數a,b,可作如下變形：
∵a+b=
（
a
）
2
+
（
b
）
2
=
（
a
）
2
+
（
b
）
2
-
2
ab
+
2
ab
=
（
a
-
b
）
2
+
2
ab

又∵
（
a
-
b
）
2
≥
0

∴
（
a
-
b
）
2
+
2
ab
≥
0
+
2
ab

即
a
+
b
≥
2
ab
．
根據上述內容，回答問題：2+3
2
2
×
3
；
4
+
1
3

2
4
×
1
3
；6+6
2
6
×
6
．（用“=”“＞”“＜”填空）
【思考驗證】
如圖1，△ABC中，∠ACB=90°，CD⊥AB于點D，CO為AB邊上中線，AD=2a,DB=2b,試根據圖形驗證
a
+
b
≥
2
ab
成立，并指出等號成立時的條件．
【探索應用】
（1）請利用上述結論解決下面問題，某園林設計師要對園林的一個區域進行設計改造，一面利用墻體將該區域用籬笆圍成中間隔有一道籬笆的矩形花圃，如圖2所示，為了圍成面積為300m²的花圃，所用的籬笆至少為多少米？
（2）如圖3，四邊形ABCD的對角線AC，BD相交于點O，△AOB，△COD的面積分別是5和16．試問四邊形ABCD的面積是否存在最小值？若存在，請直接寫出四邊形ABCD面積的最小值；若不存在，請說明理由．
組卷：995引用：2難度：0.3
解析
23．已知同一平面內的具有公共頂點C的矩形ABCD和矩形CEFG，且AB=mBC，CG=mCE，連接DG．
（1）當點E是矩形ABCD邊AB延長線上的一點時，延長BC交DG于點P．
①如圖1，若m=1，猜想線段DP與GP之間的數量關系是
；
②如圖2，若m為任意實數，則①中的猜想是否仍然成立？若成立，請給予證明；若不成立，請說明理由；
（2）當點E是平面內任意一點時，取DG的中點Q，如圖3所示，連接CQ，BE．若BC=2，CE=3，m=3，請求出CQ的取值范圍．
組卷：164引用：1難度：0.3
解析