2007年廣東省廣州市初中數學青年教師解題比賽決賽試卷

一、選擇題（共11小題，每小題4分，滿分44分）

• 1．對于實數a,下列運算正確的是（　　）

  A．2a-1=1÷（2a）	B．2a2+a=3a3
  C．（-a）3?a2=-a6	D．（-a）2×（-a2）=-a4
  組卷：66引用：1難度：0.9

  解析

• 2．給出以下三個命題：①兩個無理數的和一定是無理數；②兩個無理數的和有可能是有理數；③兩個無理數的和一定是實數．其中正確的命題是（　　）

  A．①和②

  B．①和③

  C．②和③

  D．③
  組卷：52引用：1難度：0.9

  解析

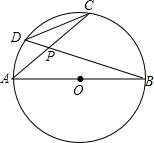• 3．如圖，AB是⊙O的直徑，弦AC、BD相交于P，則

  CD

  AB

  等于（　　）

  A．sin∠BPC

  B．cos∠BPC

  C．tan∠BPC

  D．cot∠BPC
  組卷：236引用：11難度：0.9

  解析

• 4．如圖，三個天平的托盤中形狀相同的物體質量相等．圖（1）、圖（2）所示的兩個天平處于平衡狀態，要使第三個天平也保持平衡，則需在它的右盤中放置（　　）
  

  A．3個球

  B．4個球

  C．5個球

  D．6個球
  組卷：803引用：26難度：0.9

  解析

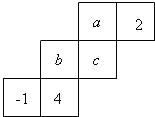• 5．如圖是一個正方體的表面展開圖，已知正方體的每一個面都有一個實數，且相對面上的兩個數互為倒數，那么代數式

  a

  c

  -

  b

  的值等于（　　）

  A． - 3 4

  B．-6

  C． 3 4

  D．6
  組卷：934引用：24難度：0.5

  解析

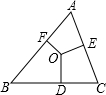• 6．如圖，O是△ABC的外心，OD⊥BC，OE⊥AC，OF⊥AB，則OD：OE：OF=（　　）

  A．a：b：c	B． 1 a ： 1 b ： 1 c
  C．cosA：cosB：cosC	D．sinA：sinB：sinC
  組卷：455引用：12難度：0.9

  解析

三、解答題（共8小題，滿分76分）

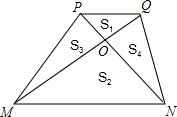• 19．如圖，在梯形PMNQ中，PQ∥MN，對角線PN和MQ相交于點O，并把梯形分成四部分，記這四部分的面積分別為S₁、S₂、S₃、S₄．試判斷S₁+S₂和S₃+S₄的大小關系，并證明你的結論．
  組卷：226引用：3難度：0.3

  解析

• 20．已知y=m²+m+4，若m為整數，在使得y為完全平方數的所有m的值中，設m的最大值為a,最小值為b,次小值為c.（注：一個數如果是另一個整數的完全平方，那么我們就稱這個數為完全平方數．）
  （1）求a、b、c的值；
  （2）對a、b、c進行如下操作：任取兩個求其和再除以

  2

  ，同時求其差再除以

  2

  ，剩下的另一個數不變，這樣就仍得到三個數．再對所得三個數進行如上操作，問能否經過若干次上述操作，所得三個數的平方和等于2008證明你的結論．
  組卷：321引用：13難度：0.1

  解析