2023-2024學年浙江省杭州十三中教育集團九年級（上）月考數學試卷（10月份）

一.選擇題（共10小題）

• 1．下列事件是隨機事件的是（　　）

  A．a2+b2=-1（其中a,b都是實數）

  B．經過有信號燈的十字路口，遇見綠燈

  C．擲一枚骰子，向上一面的點數是7

  D．任意畫一個三角形，其內角和是180°
  組卷：53引用：3難度：0.8

  解析

• 2．若拋物線y=-x²+bx+c經過點（-2，3），則c-2b的值是（　　）

  A．7

  B．-1

  C．-2

  D．3
  組卷：634引用：8難度：0.6

  解析

• 3．函數y=-2x²先向右平移3個單位，再向下平移7個單位，所得函數解析式是（　　）

  A．y=-2（x-3）2+7	B．y=-2（x-3）2-7
  C．y=-2（x+3）2+7	D．y=-2（x+3）2-7
  組卷：261引用：4難度：0.6

  解析

• 4．在平面直角坐標系中，以原點O為圓心作半徑為5的圓，則以下四個點在圓上的是（　　）

  A．（3，0）

  B．（0，6）

  C．（2，4）

  D．（3，4）
  組卷：248引用：2難度：0.5

  解析

• 5．關于二次函數y=（x-2）²+6的圖象，下列結論不正確的是（　　）

  A．拋物線的開口向上

  B．當x＜1時，y隨x的增大而減小

  C．對稱軸是直線x=2

  D．拋物線與y軸交于點（0，6）
  組卷：295引用：5難度：0.5

  解析

• 6．從標有2，3，4，5四個數字的卡片中同時抽取兩張，記其中一張卡片上的數字為x、另一張卡片上數字為y,這樣構成點P的坐標（x,y），那么點P落在雙曲線

  y

  =

  6

  x

  上的概率為（　　）

  A． 1 4

  B． 1 12

  C． 1 3

  D． 1 6
  組卷：168引用：3難度：0.5

  解析

• 7．已知點（3，y₁），（-2，y₂），（0，y₃）在拋物線y=x²-2x+c上，則y₁，y₂，y₃的大小關系是（　　）

  A．y3＜y1＜y2

  B．y1＜y3＜y2

  C．y1＜y2＜y3

  D．y2＜y3＜y1
  組卷：239引用：2難度：0.5

  解析

三.解答題（共7小題）

• 22．已知函數

  y

  1

  =

  x

  2

  -

  （

  m

  +

  2

  ）

  x

  +

  2

  m

  +

  3

  ，y₂=nx+k-2n（m,n,k為常數且n≠0）．
  （1）若函數y₁的圖象經過點A（2，4），B（-1，3）兩個點中的其中一個點，求該函數的表達式．
  （2）若函數y₁，y₂的圖象始終經過同一定點M．
  ①求點M的坐標和k的值．
  ②若m+n=-1，當-1＜x＜2時，判斷y₁與y₂的大小并說明理由．
  組卷：267引用：1難度：0.3

  解析

• 23．根據以下素材，探索完成任務．

  如何確定拱橋形狀？
  問題背景	河面上有一座拱橋，對它的形狀，同學們各抒己見．有同學說拱橋的形狀是拋物線，也有同學說是圓弧．為確定拱橋的形狀，九年級綜合實踐小組開展了一次探究活動．
  素材1	在正常水位時，小組成員對水面寬度和拱頂離水面的距離進行了測量并繪制了如圖．測得水面寬AB為16m,拱頂離水面的距離CD為4m.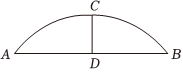
  素材2	大雨過后，水位上漲．小組成員再對水面寬度和拱頂離水面的距離進行了兩次測量發現當水面寬為12m時，水位（相對正常水位）上漲1.9m；當水面寬8m時，水位（相對正常水位）上漲3.1m.
  素材3	如何檢驗探究過程中提出的假設是否符合實際情況呢？ 定義：離差平方和是實際觀測值與預測值之間差的平方和，反映了基于假設算得的預測值與實際觀測值之間的差異．離差平方和越小，說明預測值與實際觀測值之間的誤差越小，提出的假設與實際情況更為接近．
  	問題解決
  假設1	小組成員首先假設拱橋形狀是拋物線．根據素材1建立如圖所示的直角坐標系，求該拋物線的解析式．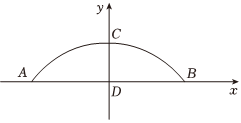
  假設2	小組成員又提出拱橋形狀可能是圓弧．請根據素材1求出該圓弧的半徑．
  分析判斷	于假設1和假設2，請分別計算水面寬12m和8m時水位上漲的預測值，直接填入下表（數據保留兩位小數），并結合素材3分別求出兩種假設下數據的離差平方和，斷拱橋更接近哪一種形狀．（參考數據： 21 ≈4.582） 水面寬12m 水面寬8m 水位上漲的實際觀測值（m） 1.90 3.10 假設1的預測值（m） 3.00 假設2的預測值（m） 2.00
  組卷：703引用：4難度：0.4

  解析