2021-2022學年黑龍江省大慶市薩爾圖區東風中學高一(下)期末數學試卷
發布:2024/11/22 23:0:1
一、單選題(共8小題,每小題5分,共40分)
-
1.復數z=3+4i,則z的共軛復數在復平面內對應的點位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限 組卷:43引用:2難度:0.8 -
2.已知角α的終邊與單位圓交于點P(
,-12),則sinα的值為( )32A. -32B. -12C. 32D. 12組卷:252引用:2難度:0.8 -
3.嫦娥五號的成功發射,實現了中國航天史上的五個“首次”,某中學為此舉行了“講好航天故事”演講比賽.若將報名的30位同學編號為01,02,……,30,利用下面的隨機數表來決定他們的出場順序,選取方法是從隨機數表第1行的第3列和第4列數字開始由左到右依次選取兩個數字,重復的跳過,則選出來的第5個個體的編號為( )
45 67 32 12 12 31 02 01 04 52 15 20 01 12 51 29
32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81A.23 B.20 C.15 D.12 組卷:148引用:4難度:0.8 -
4.已知
=(m,1),a=(2,6+m),b,則a⊥b=( )|a-b|A. 7B. 10C. 25D.5 組卷:216引用:5難度:0.8 -
5.已知平面α和α外的一條直線l,下列說法不正確的是( )
A.若l垂直于α內的兩條平行線,則l⊥α B.若l平行于α內的一條直線,則l∥α C.若l垂直于α內的兩條相交直線,則l⊥α D.若l平行于α內的無數條直線,則l∥α 組卷:132引用:3難度:0.7 -
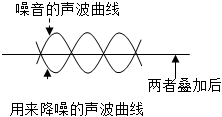 6.某智能主動降噪耳機工作的原理是利用芯片生成與噪音的相位相反的聲波,通過兩者疊加完全抵消掉噪音,如圖所示,已知噪音的聲波曲線y=Asin(ωx+φ)(其中A>0,ω>0,0<φ<2π)的振幅為1,周期為2,初相位為,則用來降噪的聲波曲線的解析式是( )π2
6.某智能主動降噪耳機工作的原理是利用芯片生成與噪音的相位相反的聲波,通過兩者疊加完全抵消掉噪音,如圖所示,已知噪音的聲波曲線y=Asin(ωx+φ)(其中A>0,ω>0,0<φ<2π)的振幅為1,周期為2,初相位為,則用來降噪的聲波曲線的解析式是( )π2A.y=sinπx B.y=-cosπx C.y=-sinπx D.y=cosπx 組卷:57引用:2難度:0.8 -
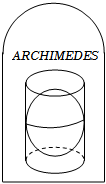 7.阿基米德(Archimedes,公元前287年-公元前212年)是古希臘偉大的數學家,物理學家和天文學家,在他墓碑上刻著的一個圓柱容器里放了一個球,該球與圓柱的兩個底面及側面均相切,如圖所示,則在該幾何體中,圓柱表面積與球表面積的比值為( )
7.阿基米德(Archimedes,公元前287年-公元前212年)是古希臘偉大的數學家,物理學家和天文學家,在他墓碑上刻著的一個圓柱容器里放了一個球,該球與圓柱的兩個底面及側面均相切,如圖所示,則在該幾何體中,圓柱表面積與球表面積的比值為( )A. 32B. 43C. 或3223D. 23組卷:101引用:3難度:0.7
四、解答題(共70分,解答應寫出文字說明、證明過程或演算步驟)
-
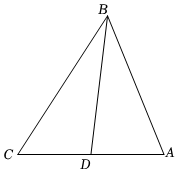 21.某市植物園平面設計如圖所示,其中區域ABD為芳香植物區,AB=40m,A=60°,區域BCD為果樹植物區,∠CBD=30°.現將芳香植物區周圍筑起小竹欄.
21.某市植物園平面設計如圖所示,其中區域ABD為芳香植物區,AB=40m,A=60°,區域BCD為果樹植物區,∠CBD=30°.現將芳香植物區周圍筑起小竹欄.
(1)若AD=20m,求小竹欄的長度(△ABD的周長);
(2)設∠ABD=45°時,求果樹植物區的面積.組卷:48引用:1難度:0.5 -
22.已知O為坐標原點,對于函數f(x)=asinx+bcosx,稱向量
為函數f(x)的伴隨向量,同時稱函數f(x)為向量OM=(a,b)的伴隨函數.OM
(1)若函數,求函數g(x)的伴隨向量;g(x)=sinx+2cos(x+π3)
(2)若函數f(x)的伴隨向量為(1,1),且函數f(x)在(0,x1)上有且只有一個零點,求x1的最大值;
(3)若函數f(x)的伴隨向量為,h(x)=f(x)+1,若實數m,n,p使得mh(x)+nh(x-p)=1對任意實數x恒成立,求(3,1)的值.cospm+n組卷:48引用:3難度:0.5


