2021-2022學年江蘇省南通市如皋中學高一（上）期末數學試卷

一、單項選擇題（本大題共8小題，每小題5分，共計40分．在每小題給出的四個選項中，只有一個是符合題目要求的，請把答案填涂在答題卡相應位置上）

• 1．已知函數f（x）滿足f（3^x）=log₂x,則f（9）=（　　）

  A．-1

  B．1

  C．2

  D．0
  組卷：97引用：6難度：0.8

  解析

• 2．已知U=R，集合A={-1，1}，B={x|x²＜4}，則下列關系正確的是（　　）

  A．A∪B=A

  B．A∩B=?

  C．?UA??UB

  D．?UB??UA
  組卷：60引用：1難度：0.7

  解析

• 3．我國著名數學家華羅庚先生曾說：“數缺形時少直觀，形缺數時難入微”．在數學的學習和研究過程中，常用函數圖象來研究函數的性質，也經常用函數解析式來分析函數的圖象特征．函數y=|x|sinx在[-π，π]上的圖象大致是（　　）

  A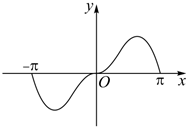．	B．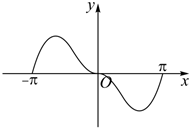
  C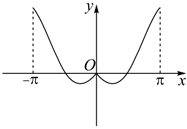．	D．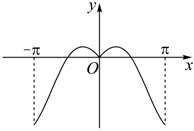
  組卷：125引用：4難度：0.8

  解析

• 4．將y=sin（3x-

  3

  π

  4

  ）圖象上每一個點的橫坐標變為原來的3倍（縱坐標不變），得到y=g（x）的圖象，再將y=g（x）圖象向左平移

  3

  π

  4

  ，得到y=φ（x）的圖象，則y=φ（x）的解析式為（　　）

  A．y=sinx	B．y=cosx
  C．y=sin9x	D．y=sin（9x- 3 π 2 ）
  組卷：545引用：3難度：0.8

  解析

• 5．解析數論的創始人狄利克雷在數學領域成就顯著，對函數論、位勢論和三角級數論都有重要貢獻．以他名字命名的狄利克雷函數D（x）=

  1 ， x ∈ Q

  0 ， x ∈ ? R Q

  ，以下結論錯誤的是（　　）

  A． D （ 2 ） ＜ D （ 1 ）

  B．函數y=D（x）不是周期函數

  C．D（D（x））=1

  D．函數y=D（x）在（-∞，+∞）上不是單調函數
  組卷：213引用：4難度：0.5

  解析

• 6．設a為實數，定義在R上的偶函數f（x）滿足：①f（x）在[0，+∞）上為增函數；②f（2a）＜f（a+1），則實數a的取值范圍為（　　）

  A．（-∞，1）	B．（- 1 3 ，1）
  C．（-1， 1 3 ）	D．（- ∞ ，- 1 3 ）∪（1，+∞）
  組卷：484引用：4難度：0.6

  解析

• 7．已知x∈（

  π

  2

  ，π），sinx+sin（x+

  π

  2

  ）=

  10

  5

  ，則tanx=（　　）

  A．-3

  B．- 1 3

  C．-3或- 1 3

  D．- 1 2
  組卷：341引用：2難度：0.7

  解析

四、解答題（本大題共6小題，共計70分．請在答題卡指定區域內作答．解答時應寫出文字說明、證明過程或演算步驟）

• 21．已知集合D={（x₁，x₂）|x₁+x₂=1，x₁＞0，x₂＞0}．
  （1）設u=x₁x₂，求u的取值范圍；
  （2）對任意（x₁，x₂）∈D，證明：（x₁-

  1

  x

  1

  ）（x₂-

  1

  x

  2

  ）≤

  9

  4

  ．
  組卷：124引用：2難度：0.5

  解析

• 22．數學家研究發現，音叉發出的聲音（音叉附近空氣分子的振動）可以用數學模型y=Asinωt（ω＞0，t＞0）來刻畫．1807年，法國數學家傅里葉用一個純粹的數學定理表述了任何周期性聲音的公式是形如Asinωt的簡單正弦函數之和．若某種聲音的模型是函數f（t）=sin2t（t＞0），g（t）=2f²（t）-af（t），（t＞0）．
  （1）求函數f（t）在（0，

  7

  π

  12

  ]上的值域；
  （2）若a≥0，試研究函數g（t）在（0，

  7

  π

  12

  ]上的零點個數，并說明理由．
  組卷：158引用：3難度：0.5

  解析