2021-2022學年天津市武清區英華國際中學高二（上）期中數學試卷

一、選擇題

• 1．已知橢圓

  x

  2

  m

  -

  2

  +

  y

  2

  10

  -

  m

  =

  1

  的一個焦點為（2，0），則m等于（　　）

  A．8

  B．7

  C．6

  D．5
  組卷：345引用：1難度：0.8

  解析

• 2．平面α的一個法向量是

  n

  =（

  1

  2

  ，-1，

  1

  3

  ），平面β的一個法向量是

  m

  =（-3，6，-2），則平面α與平面β的關系是（　　）

  A．平行

  B．重合

  C．平行或重合

  D．垂直
  組卷：118引用：8難度：0.8

  解析

• 3．已知直線l₁：mx+4y-2=0與l₂：2x-5y+n=0互相垂直，其垂足為（1，p），則m+n-p的值為（　　）

  A．4

  B．-16

  C．0

  D．20
  組卷：2302引用：14難度：0.9

  解析

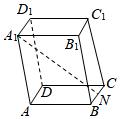• 4．如圖所示，在平行六面體ABCD-A₁B₁C₁D₁中，設

  A

  A

  1

  =

  a

  ，

  AB

  =

  b

  ，

  AD

  =

  c

  ，N是BC的中點，則

  A

  1

  N

  等于（　　）

  A．- a + b + 1 2 c

  B．- a + b + c

  C．- a - b + 1 2 c

  D． a - b + 1 2 c
  組卷：1391引用：11難度：0.8

  解析

• 5．已知圓C：x²+y²+2x-2my-4-4m=0（m∈R），則當圓C的面積最小時，圓上的點到坐標原點的距離的最大值為（　　）

  A． 5

  B．6

  C． 5 - 1

  D． 5 + 1
  組卷：2227引用：22難度：0.8

  解析

• 6．若點O和點F分別為橢圓

  x

  2

  4

  +

  y

  2

  3

  =1的中心和左焦點，點P為橢圓上的任意一點，則

  OP

  ?

  FP

  的最大值為（　　）

  A．2

  B．3

  C．6

  D．8
  組卷：3851引用：119難度：0.9

  解析

三、解答題（共5小題，滿分0分）

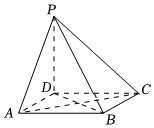• 19．如圖，四棱錐P-ABCD的底面是平行四邊形，PD⊥AB，AC=BD．
  （1）證明：平面PAD⊥平面ABCD；
  （2）若AD=2AB=6，

  PA

  =

  PD

  =

  3

  2

  ，在此條件下求下面問題：
  ①直線PD和AC所成角的余弦值，
  ②試在棱PD上確定一點M，使得平面PAB與平面MAC所成銳二面角的余弦值為

  15

  5

  ．
  組卷：49引用：1難度：0.6

  解析

• 20．已知橢圓

  E

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的兩個焦點F₁（-c,0），F₂（c,0）與短軸的一個端點構成一個等邊三角形，且直線3x+4y+6=0與圓x²+（y-c）²=a²相切．
  （1）求橢圓E的方程；
  （2）已知過橢圓C的左頂點A的兩條直線l₁，l₂分別交橢圓C于M，N兩點，且l₁⊥l₂，求證：直線MN過定點，并求出定點坐標；
  （3）在（2）的條件下求△AMN面積的最大值．
  組卷：137引用：2難度：0.5

  解析