2023年山東省日照市校際聯考高考數學一模試卷

一、單項選擇題。本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合A={x|x＜2}，B={x|x²-2x-3≤0}，則A∪B=（　　）

  A．[-1，2）

  B．（2，3]

  C．（-1，3]

  D．（-∞，3]
  組卷：198引用：2難度：0.7

  解析

• 2．已知復數z=

  2

  +

  6

  i

  1

  -

  i

  ，i為虛數單位，則|z|=（　　）

  A．2 2

  B．2 3

  C．2 5

  D．2 6
  組卷：271引用：9難度：0.8

  解析

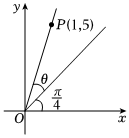• 3．在平面直角坐標系xOy中，角θ的大小如圖所示，則tanθ=（　　）

  A． 3 2

  B． 4 3

  C．1

  D． 2 3
  組卷：184引用：1難度：0.7

  解析

• 4．紅燈籠，起源于中國的西漢時期，兩千多年來，每逢春節人們便會掛起象征美好團圓意義的紅燈籠，營造一種喜慶的氛圍．如圖1，某球形燈籠的輪廓由三部分組成，上下兩部分是兩個相同的圓柱的側面，中間是球面除去上下兩個相同球冠剩下的部分．如圖2，球冠是由球面被平面截得的一部分，垂直于截面的直徑被截得的部分叫做球冠的高，若球冠所在球面的半徑為R，球冠的高為h,則球冠的面積S=2πRh.如圖1，已知該燈籠的高為58cm,圓柱的高為5cm,圓柱的底面圓直徑為14cm,則圍成該燈籠中間球面部分所需布料的面積為（　　）
  

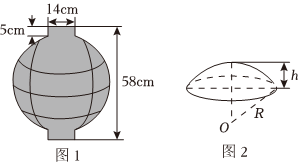
  A．1940πcm2

  B．2350πcm2

  C．2400πcm2

  D．2540πcm2
  組卷：463引用：8難度：0.7

  解析

• 5．已知正六邊形ABCDEF的邊長為2，P是正六邊形ABCDEF邊上任意一點，則

  PA

  ?

  PB

  的最大值為（　　）

  A．13

  B．12

  C．8

  D． 2 3
  組卷：545引用：5難度：0.6

  解析

• 6．已知x＞0，y＞0，設命題p：2^x+2^y≥4，命題q：xy≥1，則p是q的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：123引用：4難度：0.8

  解析

• 7．已知數列{a_n}的前n項和為S_n，且滿足a₁=1，a_na_n+1=2S_n，設

  b

  n

  =

  a

  n

  3

  n

  ，若存在正整數p,q（p＜q），使得b₁，b_p，b_q成等差數列，則（　　）

  A．p=1

  B．p=2

  C．p=3

  D．p=4
  組卷：157引用：1難度：0.6

  解析

四、解答題。共70分。解答應寫出文字說明，證明過程或演算步驟。

• 21．第22屆世界杯于2022年11月21日到12月18日在卡塔爾舉辦．在決賽中，阿根廷隊通過點球戰勝法國隊獲得冠軍．
  （1）撲點球的難度一般比較大．假設罰點球的球員會等可能地隨機選擇球門的左、中、右三個方向射門，門將也會等可能地隨機選擇球門的左、中、右三個方向來撲點球，而且門將即使方向判斷正確也有

  2

  3

  的可能性撲不到球．不考慮其它因素，在一次點球大戰中，求門將在前三次撲到點球的個數X的分布列和期望；
  （2）好成績的取得離不開平時的努力訓練，甲、乙、丙三名前鋒隊員在某次傳接球的訓練中，球從甲腳下開始，等可能地隨機傳向另外2人中的1人，接球者接到球后再等可能地隨機傳向另外2人中的1人，如此不停地傳下去，假設傳出的球都能接住，記第n次傳球之前球在甲腳下的概率為p_n，易知p₁=1，p₂=0．
  ①證明：

  {

  p

  n

  -

  1

  3

  }

  為等比數列；
  ②設第n次傳球之前球在乙腳下的概率為q_n，比較p₁₀與q₁₀的大小．
  組卷：541引用：8難度：0.6

  解析

• 22．已知函數f（x）=e^x-a，g（x）=lnx+a（a∈R）．
  （1）若直線y=x是y=g（x）的切線，函數

  F

  （

  x

  ）

  =

  f （ x ） ， x ≤ 1

  g （ x ） ， x ＞ 1

  總存在x₁＜x₂，使得F（x₁）+F（x₂）=2，求x₁+F（x₂）的取值范圍；
  （2）設G（x）=f（x）-g（x），若|G（x）|=b恰有三個不等實根，證明：

  a

  -

  1

  a

  ＜

  b

  ＜

  2

  a

  -

  2

  ．
  組卷：112引用：1難度：0.2

  解析