2023-2024學年貴州省高一（上）期中聯考數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．若集合A=（-4，1），B=（-2，5），A∩B=M，則（　　）

  A．-3∈M

  B．-2∈M

  C． 2 3 ∈ M

  D． 4 3 ∈ M
  組卷：6引用：3難度：0.7

  解析

• 2．若函數f（x）的定義域為（-3，6），則函數y=f（2x）的定義域為（　　）

  A．（-1，2）

  B． （ - 3 2 ， 3 ）

  C．（-6，12）

  D．（-9，18）
  組卷：101引用：5難度：0.8

  解析

• 3．若命題p：菱形是中心對稱圖形，則（　　）

  A．p是全稱量詞命題，且p的否定：所有的菱形不是中心對稱圖形

  B．p是全稱量詞命題，且p的否定：有些菱形不是中心對稱圖形

  C．p是存在量詞命題，且p的否定：所有的菱形不是中心對稱圖形

  D．p是存在量詞命題，且p的否定：有些菱形不是中心對稱圖形
  組卷：10引用：2難度：0.8

  解析

• 4．若函數f（x+1）=x²-5，則f（x）=（　　）

  A．x2+2x-6

  B．x2+2x-4

  C．x2-2x-6

  D．x2-2x-4
  組卷：48引用：4難度：0.8

  解析

• 5．“x-y＞-1”是“x³+x＞x²y+y”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：15引用：3難度：0.8

  解析

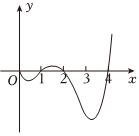• 6．已知奇函數f（x）在[0，+∞）上的部分圖象如圖所示，則不等式f（x）≥0在[-4，4]上的解集為（　　）

  A．[-4，-2]∪[1，2]∪{4}	B．[-3，-2]∪[-1，0]∪[1，2]∪{-4，4}
  C．[-2，-1]∪[1，2]∪{-4，4}	D．[-4，-2]∪[-1，0]∪[1，2]∪{4}
  組卷：15引用：1難度：0.8

  解析

• 7．若命題“?x∈[-2，1]，ax²+2ax+3a＞1”為假命題，則a的最大值為（　　）

  A． 1 6

  B． 1 3

  C． 1 2

  D． 1 4
  組卷：38引用：3難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知函數f（x）=x²-（2m+1）x+m（m+1）．
  （1）當m=0時，求f（x）的零點；
  （2）若f（x）只有一個零點在（1，3）內，求m的取值范圍．
  組卷：118引用：1難度：0.8

  解析

• 22．對于函數f（x），如果對其定義域D中任意給定的實數，都有-x∈D，且f（x）f（-x）=1，就稱f（x）為“倒函數”．
  （1）判斷函數

  f

  （

  x

  ）

  =

  8

  +

  x

  3

  8

  -

  x

  3

  （

  x

  2

  ≠

  4

  ）

  是否為“倒函數”，并說明理由；
  （2）若定義域為R的倒函數g（x）的圖象是一條連續不斷的曲線，且g（x）在（-∞，0）上單調遞增，?x∈（-∞，0），g（x）＞0．
  ①根據定義，研究g（x）在R上的單調性；
  ②若

  g

  （

  -

  2

  ）

  =

  1

  2

  ，函數h（x）=[g（x）]²+[g（-x）]²-g（x）-g（-x），求h（x）在[-2，2]上的值域．
  組卷：167引用：7難度：0.3

  解析