2022-2023學年黑龍江省大慶市薩爾圖區祥閣學校九年級（下）月考數學試卷（3月份）

一、選擇題（每題3分，共30分）

• 1．下列運算中，正確的是（　　）

  A．x3+x4=x7	B．2x2?3x4=6x8
  C．（-3x2y）2=-9x4y2	D． 5 × 6 = 30
  組卷：1356引用：15難度：0.8

  解析

• 2．如圖圖形是中心對稱圖形的是（　　）

  A．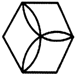

  B．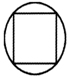

  C．

  D．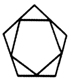
  組卷：54引用：4難度：0.9

  解析

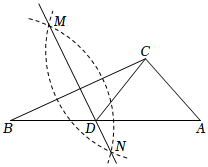• 3．如圖，在已知的△ABC中，按以下步驟作圖：①分別以B，C為圓心，以大于

  1

  2

  BC的長為半徑作弧，兩弧相交于兩點M，N；②作直線MN交AB于點D，連接CD．若CD=AC，∠A=50°，則∠ACB的度數為（　　）

  A．105°

  B．100°

  C．95°

  D．90°
  組卷：1157引用：39難度：0.7

  解析

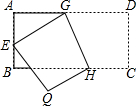• 4．如圖，將矩形ABCD沿GH折疊，點C落在點Q處，點D落在AB邊上的點E處，若∠AGE=32°，則∠GHC等于（　　）

  A．112°

  B．110°

  C．108°

  D．106°
  組卷：4875引用：44難度：0.7

  解析

• 5．已知點（a,m），（b,n）在反比例函數y=-

  2

  x

  的圖象上，且a＞b,則（　　）

  A．m＞n	B．m＜n
  C．m=n	D．m、n的大小無法確定
  組卷：673引用：5難度：0.6

  解析

• 6．已知關于x的分式方程

  x

  x

  -

  2

  -4=

  k

  2

  -

  x

  的解為正數，則k的取值范圍是（　　）

  A．-8＜k＜0

  B．k＞-8且k≠-2

  C．k＞-8且k≠2

  D．k＜4且k≠-2
  組卷：2092引用：19難度：0.7

  解析

• 7．已知a,b是一元二次方程x²-2x-2020=0的兩個根，則a²+2b-3的值等于（　　）

  A．2020

  B．2021

  C．2022

  D．2023
  組卷：639引用：3難度：0.6

  解析

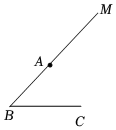• 8．題目：“如圖，∠B=45°，BC=2，在射線BM上取一點A，設AC=d,若對于d的一個數值，只能作出唯一一個△ABC，求d的取值范圍．”對于其答案，甲答：d≥2，乙答：d=1.6，丙答：d=

  2

  ，則正確的是（　　）

  A．只有甲答的對

  B．甲、丙答案合在一起才完整

  C．甲、乙答案合在一起才完整

  D．三人答案合在一起才完整
  組卷：1192引用：3難度：0.5

  解析

• 9．若滿足

  1

  2

  ＜x≤1的任意實數x,都能使不等式2x³-x²-mx＞2成立，則實數m的取值范圍是（　　）

  A．m＜-1

  B．m≥-5

  C．m＜-4

  D．m≤-4
  組卷：1998引用：9難度：0.7

  解析

三、解答題（共66分）

• 27．在△ABC中，∠ACB=90°，D為△ABC內一點，連接BD，DC，延長DC到點E，使得CE=DC．
  （1）如圖1，延長BC到點F，使得CF=BC，連接AF，EF．若AF⊥EF，求證：BD⊥AF；
  （2）連接AE，交BD的延長線于點H，連接CH，依題意補全圖2．若AB²=AE²+BD²，用等式表示線段CD與CH的數量關系，并證明．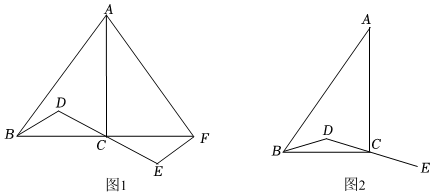
  
  組卷：5520引用：22難度：0.6

  解析

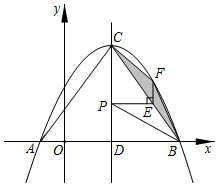• 28．已知拋物線y=ax²+bx+c與x軸交于A（-1，0），B（5，0）兩點，C為拋物線的頂點，拋物線的對稱軸交x軸于點D，連接AC，BC，且tan∠CBD=

  4

  3

  ，如圖所示．
  （1）求拋物線的解析式；
  （2）設P是拋物線的對稱軸上的一個動點．
  ①過點P作x軸的平行線交線段BC于點E，過點E作EF⊥PE交拋物線于點F，連接FB、FC，求△BCF的面積的最大值；
  ②連接PB，求

  3

  5

  PC+PB的最小值．
  組卷：2246引用：9難度：0.2

  解析