2022-2023學年遼寧省沈陽120中高一（下）第一次質檢數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一個符合題目要求

• 1．已知點A是單位圓與x軸正半軸的交點，點B在第二象限．記∠AOB=θ且sinθ=

  3

  5

  ，則

  sin

  （

  π

  +

  θ

  ）

  +

  2

  sin

  （

  π

  2

  -

  θ

  ）

  2

  tan

  （

  π

  -

  θ

  ）

  =（　　）

  A． 22 15

  B． 2 3

  C． - 22 15

  D． - 2 3
  組卷：321引用：3難度：0.8

  解析

• 2．已知向量

  a

  =（2，1），

  b

  =（1，-1），向量

  a

  在

  b

  方向上的投影向量為（　　）

  A．（2，-2）

  B．（ 1 2 ， - 1 2 ）

  C．（ 2 5 ， 1 5 ）

  D．（ 2 2 ， - 2 2 ）
  組卷：559引用：8難度：0.8

  解析

• 3．已知函數f（x）=x²．令

  a

  =

  f

  （

  sin

  2

  π

  7

  ）

  ，

  b

  =

  f

  （

  cos

  5

  π

  7

  ）

  ，

  c

  =

  f

  （

  tan

  5

  π

  7

  ）

  ，則（　　）

  A．c＜a＜b

  B．a＜b＜c

  C．b＜c＜a

  D．b＜a＜c
  組卷：75引用：2難度：0.7

  解析

• 4．已知單位向量

  a

  ，

  b

  滿足

  a

  ?

  b

  =

  -

  1

  4

  ，若向量

  c

  =

  a

  +

  2

  b

  ，則

  ?

  a

  ，

  c

  ?

  =（　　）

  A． arccoc 1 3

  B． arccos 2 3

  C． arccos 1 4

  D． arccos 3 3
  組卷：27引用：2難度：0.8

  解析

• 5．已知曲線C₁：y=cosx,C₂：y=sin（2x+

  2

  π

  3

  ），則下面結論正確的是（　　）

  A．把C1上各點的橫坐標伸長到原來的2倍，縱坐標不變，再把得到的曲線向右平移 π 6 個單位長度，得到曲線C2

  B．把C1上各點的橫坐標伸長到原來的2倍，縱坐標不變，再把得到的曲線向左平移 π 12 個單位長度，得到曲線C2

  C．把C1上各點的橫坐標縮短到原來的 1 2 ，縱坐標不變，再把得到的曲線向右平移 π 6 個單位長度，得到曲線C2

  D．把C1上各點的橫坐標縮短到原來的 1 2 ，縱坐標不變，再把得到的曲線向左平移 π 12 個單位長度，得到曲線C2
  組卷：4669引用：37難度：0.9

  解析

• 6．已知函數f（x）=tan（ωx-φ）（ω＞0，0＜φ＜π）與直線y=a交于A，B兩點，且線段AB長度的最小值為

  π

  3

  ，若將函數f（x）的圖象向左平移

  π

  12

  個單位后恰好關于原點對稱，則φ的最大值為（　　）

  A． π 8

  B． π 4

  C． 3 π 4

  D． 7 π 8
  組卷：242引用：5難度：0.5

  解析

• 7．若θ為第二象限角，且

  tan

  （

  θ

  -

  π

  ）

  =

  -

  1

  2

  ，則

  1

  +

  cosθ

  1

  -

  sin

  （

  π

  2

  -

  θ

  ）

  -

  1

  -

  cosθ

  1

  +

  sin

  （

  θ

  -

  3

  π

  2

  ）

  的值是（　　）

  A．4

  B．-4

  C． 1 4

  D． - 1 4
  組卷：1303引用：7難度：0.6

  解析

四、解答題：本大題共6小題，其中17題滿分70分，其余各題滿分70分

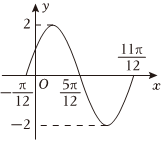• 21．函數f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，

  |

  φ

  |

  ＜

  π

  2

  ）的部分圖象如圖所示，把函數f（-x）的圖象向右平移

  π

  4

  個單位，得到函數g（x）的圖象．
  （1）當x∈R時，求函數g（x）的單調遞減區間；
  （2）對于

  ?

  x

  1

  ∈

  [

  -

  π

  12

  ，

  π

  3

  ]

  ，是否總存在唯一的實數

  x

  2

  ∈

  [

  π

  6

  ，

  3

  4

  π

  ]

  ，使得f（x₁）+g（x₂）=m成立？若存在，求出實數m的值或取值范圍；若不存在，說明理由．
  組卷：190引用：5難度：0.4

  解析

• 22．在△ABC中，CA=6，AB=8，

  ∠

  BAC

  =

  π

  2

  ，D為邊BC中點．
  （1）求

  AD

  ?

  CB

  的值；
  （2）若點P滿足

  CP

  =

  λ

  CA

  （λ∈R），求

  PB

  ?

  PC

  的最小值；
  （3）若點P在∠BAC的角平分線上，且滿足

  PA

  =

  m

  PB

  +

  n

  PC

  （m,n∈R），若1≤n≤2，求

  |

  PA

  |

  的取值范圍．
  組卷：110引用：2難度：0.5

  解析