2023年天津市高考數學最后一卷

一、選擇題

• 1．設全集為U={1，2，3，4，5，6}，?_UA={2，3，5}，B={2，5，6}，則A∩（?_UB）=（　　）

  A．{1，4}

  B．{2，5}

  C．{6}

  D．{1，3，4，6}
  組卷：440引用：6難度：0.8

  解析

• 2．已知非零向量

  a

  ，

  b

  ，則“

  a

  與

  b

  共線”是“

  |

  a

  -

  b

  |

  ≤

  |

  |

  a

  |

  -

  |

  b

  |

  |

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：518引用：6難度：0.7

  解析

• 3．函數

  f

  （

  x

  ）

  =

  （

  2

  x

  -

  2

  -

  x

  ）

  cosx

  x

  2

  -

  4

  的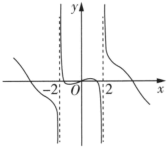部分圖象為（　　）

  A．	B．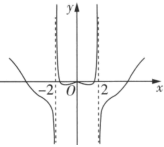
  C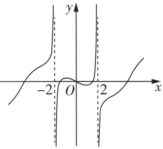．	D．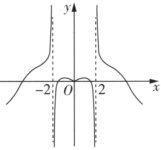
  組卷：291引用：6難度：0.7

  解析

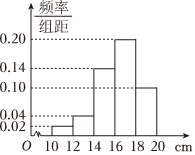• 4．某鄉鎮為推動鄉村經濟發展，優化產業結構，逐步打造高品質的農業生產，在某試驗區種植了某農作物．為了解該品種農作物長勢，在實驗區隨機選取了100株該農作物苗，經測量，其高度（單位：cm）均在區間[10，20]內，按照[10，12），[12，14），[14，16），[16，18），[18，20]分成5組，制成如圖所示的頻率分布直方圖，記高度不低于16cm的為“優質苗”．則所選取的農作物樣本苗中，“優質苗”株數為（　　）

  A．20

  B．40

  C．60

  D．88
  組卷：295引用：7難度：0.9

  解析

• 5．若a=log_0.30.4，b=1.2^0.3，c=log_2.10.9，則（　　）

  A．a＞b＞c

  B．b＞c＞a

  C．a＞c＞b

  D．b＞a＞c
  組卷：586引用：10難度：0.6

  解析

• 6．若

  f

  （

  x

  ）

  =

  ln

  |

  m

  -

  2

  x

  +

  3

  |

  -

  n

  是奇函數，則mn=（　　）

  A． - ln 3 3

  B． ln 3 3

  C． - ln 6 6

  D． ln 6 6
  組卷：435引用：3難度：0.7

  解析

三、解答題：本大題共5小題，共75分．解答應寫出文字說明，證明過程或演算步驟．

• 19．已知數列{a_n}的前n項和為S_n，滿足：

  2

  S

  n

  n

  =

  a

  n

  +

  1

  （

  n

  ∈

  N

  *

  ）

  ．
  （1）求證：數列{a_n}為等差數列；
  （2）若a₂=3，數列{b_n}滿足b₁=a₁，b₃=a₃-1，lgb_n+lgb_n+2=2lgb_n+1（n∈N^*），記T_n為{b_n}的前n項和，求證：T_n?T_n+2＜

  T

  2

  n

  +

  1

  ；
  （3）在（2）的前提下，記c_n=

  （ 6 n - 7 ） b n a n a n + 2 ， n 為奇數

  lo g 2 b n + 1 ， n 為偶數

  ，數列{c_n}的前2n項和為K_2n，若不等式（-1）ⁿλ+

  4

  n

  4

  n

  +

  1

  ＜

  K

  2

  n

  對一切n∈N^*恒成立，求λ的取值范圍．
  組卷：508引用：3難度：0.2

  解析

• 20．已知函數

  f

  （

  x

  ）

  =

  2

  lnx

  -

  4

  x

  -

  a

  x

  2

  -

  2

  ，a∈R．
  （1）求函數f（x）的單調區間；
  （2）若函數f（x）有唯一的極值點x₀，
  ①求實數a取值范圍；
  ②證明：

  x

  2

  0

  ?

  f

  （

  x

  0

  ）

  +

  2

  x

  2

  0

  ?

  e

  1

  -

  x

  0

  +

  1

  ≥

  0

  ．
  組卷：204引用：3難度：0.3

  解析