2022-2023學(xué)年浙江省溫州市九年級（上）第二次月考數(shù)學(xué)試卷
發(fā)布：2024/5/1 8:0:8
一、選擇題（本題有10小題，每小題4分，共40分，每小題只有一個選項是正確的，選擇正確才給分）
-
1．設(shè)正方形ABCD的中心為點O，在以五個點A、B、C、D、O為頂點所構(gòu)成的所有三角形中任意取出兩個，它們的面積相等的概率為（ ）
組卷：232引用：5難度：0.9 -
2．已知二次函數(shù)y=ax2-bx（a≠0），經(jīng)過點P（m,2）．當(dāng)y≥-1時，x的取值范圍為x≤t-1或x≥-3-t.則如下四個值中有可能為m的是（ ）
組卷：4457引用：17難度：0.3 -
3．△ABC中，AC=2，BC=3，AD⊥AB，AD=2AB，連接CD，則CD的最大值為（ ）
組卷：40引用：2難度：0.4 -
4．點P（x1，y1），Q（x2，y2）在拋物線y=ax2-4ax+2（a＞0）上，對于t＜x1＜t+1，t+2＜x2＜t+3，有y1≠y2，則t的取值范圍是（ ）
組卷：176引用：1難度：0.5 -
5．已知拋物線y=ax2+bx+c（a≠0）交x軸于點A（1，0），B（3，0）．P1（x1，y1），P2（x2，y2）是拋物線上兩個點．若|x1-2|＞|x2-2|＞1，則下列結(jié)論一定正確的是（ ）
組卷：513引用：3難度：0.6 -
6．如圖，在△ABC中，∠ACB=90°，AC=8，BC=6，P是AC上的一點，PH⊥AB于點H，以PH為直徑作⊙O，當(dāng)CH與PB的交點落在⊙O上時，AP的值為（ ）組卷：1363引用：4難度：0.3 -
7．如圖，已知在正方形ABCD中，連接AC，在AC上截取AE=AD，作△ADE的外接圓交AB于點F，連接DF交AC于點M，連接EF，下列選項不正確的是（ ）組卷：340引用：2難度：0.4 -
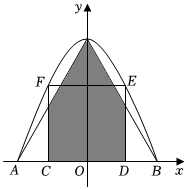8．如圖，拋物線與x軸交于點A，B，與y軸交于點G，正方形CDEF的邊CD在x軸上，E，F(xiàn)在拋物線上，連結(jié)GA，GB，△ABG是正三角形，AB=2，則陰影部分的面積為（ ）組卷：210引用：4難度：0.5 -
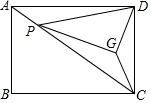9．如圖，在矩形ABCD中，AB=2，BC=4，P是對角線AC上的動點，連接DP，將直線DP繞點P順時針旋轉(zhuǎn)，使旋轉(zhuǎn)角等于∠DAC，且DG⊥PG，即∠DPG=∠DAC．連接CG，則CG最小值為（ ）組卷：1203引用：2難度：0.3 -
10．勾股定理是幾何中一個重要定理．著名數(shù)學(xué)家畢達哥拉斯用如圖①所示的圖形驗證了勾股定理，把圖①放入矩形內(nèi)得到圖②，∠ACB=90°，BC=2AC，E，F(xiàn)，G，H，I都在矩形MNOP的邊上，則的值為（ ）MNMP組卷：480引用：2難度：0.2
二、填空題（本題有6小題，每小題5分，共30分）
-
11．A，B，C，D，E，F(xiàn)，G，H是⊙O上的八個等分點，任取三點能構(gòu)成直角三角形的概率是．
組卷：202引用：4難度：0.9
五、填空題（共6小題，每小題0分，滿分0分）
-
34．在△ABC中，∠ACB=90°，D是BC邊上一點，P是AD延長線上一點，連接BP，CP．
（1）如圖1，若∠APB=90°，求證：CD?BD=AD?PD；
（2）如圖2，AC=BC=3，∠APB=45°．
①若CD=1，求AD?PD的值；
②如圖3，M為PB的中點，當(dāng)點D從點B運動到點C的過程中，直接寫出點M運動的路徑長．
組卷：404引用：2難度：0.3 -
35．已知，如圖1，⊙O是四邊形ABCD的外接圓，連接OC交對角線BD于點F，延長AO交BD于點E，OE=OF
（1）求證：BE=FD；
（2）如圖2，若∠EOF=90°，BE=EF，⊙O的半徑AO=2，求四邊形ABCD的面積；5
（3）如圖3，若AD=BC，
①求證：AB?CD+BC2=BD2；
②若AB?CD=AO2=12，直接寫出CD的長．組卷：406引用：2難度：0.1