2022-2023學年河南省鄭州第四高級中學高一（上）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．命題“?x∈R，x²＞1-2x”的否定是（　　）

  A．?x∈R，x2＜1-2x	B．?x∈R，x2≤1-2x
  C．?x∈R，x2≤1-2x	D．?x∈R，x2＜1-2x
  組卷：312引用：19難度：0.8

  解析

• 2．函數

  f

  （

  x

  ）

  =

  x

  （

  2

  -

  x

  ）

  +

  （

  x

  -

  1

  ）

  0

  的定義域為（　　）

  A．[0，2]	B．[1，2]
  C．[0，1）∪（1，2]	D．（0，1）∪（1，2）
  組卷：714引用：6難度：0.8

  解析

• 3．下列命題為假命題的是（　　）

  A．若a＞b,則a-c＞b-c

  B．若a＞b＞0，c＞d＞0，則ac＞bd＞0

  C．若a＞b＞0，則a2＞ab

  D．若a＞b,c＞d,則a-c＞b-d
  組卷：213引用：8難度：0.8

  解析

• 4．已知角α終邊上一點P（-1，2），則cos（π-α）=（　　）

  A． - 5 5

  B． - 2 5 5

  C． 5 5

  D． 2 5 5
  組卷：398引用：3難度：0.8

  解析

• 5．已知

  a

  =

  2

  lo

  g

  3

  2

  2

  ，b=0.3^0.01，

  c

  =

  lo

  g

  2

  2

  ，則a,b,c的大小關系為（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．c＜a＜b

  D．a＜c＜b
  組卷：161引用：8難度：0.7

  解析

• 6．函數

  f

  （

  x

  ）

  =

  e

  x

  e

  2

  x

  -

  1

  的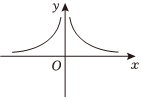大致圖象為（　　）

  A．

  B．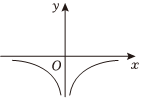

  C．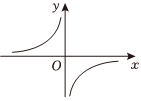

  D．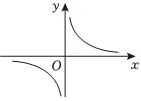
  組卷：758引用：12難度：0.7

  解析

• 7．已知α∈（0，π），β∈（0，π），

  sin

  （

  α

  -

  β

  ）

  =

  3

  4

  ，

  tanα

  tanβ

  =

  -

  5

  ，則α+β=（　　）

  A． 1 6 π

  B． 11 6 π

  C． 7 6 π

  D． 5 6 π
  組卷：524引用：5難度：0.6

  解析

四、解答題：本題共6小題，共70分．解答應寫出必要的文字說明、證明過程及演算步驟．

• 21．函數

  f

  （

  x

  ）

  =

  2

  sin

  （

  2

  x

  -

  π

  4

  ）

  +

  2

  sinxcosx

  +

  2

  si

  n

  2

  x

  -

  1

  ，x∈R．
  （1）把f（x）的解析式改寫為f（x）=Asin（ωx+φ）（A＞0，ω＞0）的形式；
  （2）求f（x）的最小正周期，并求f（x）在區間

  [

  0

  ，

  11

  π

  24

  ]

  上的最大值和最小值；
  （3）把y=f（x）圖象上所有的點的橫坐標變為原來的2倍得到函數y=g（x）的圖象，再把函數y=g（x）圖象上所有的點向右平移

  π

  4

  個單位長度，得到函數y=h（x）的圖象，若函數

  y

  =

  h

  （

  x

  ）

  +

  2

  在區間[0，m]上至少有30個零點，求m的最小值．
  組卷：296引用：2難度：0.5

  解析

• 22．設a∈R，已知函數

  f

  （

  x

  ）

  =

  2

  x

  +

  a

  2

  x

  -

  a

  為奇函數．
  （1）求實數a的值；
  （2）若a＜0，判斷并證明函數f（x）的單調性；
  （3）在（2）的條件下，函數f（x）在區間[m,n]（m＜n）上的值域是[k?2^m，k?2ⁿ]（k∈R），求k的取值范圍．
  組卷：328引用：10難度：0.6

  解析