2022-2023學年北京市豐臺區高二（下）期末數學試卷

一、選擇題共10小題，每小題4分，共40分。在每小題列出的四個選項中，選出符合題目要求的一項。

• 1．在等差數列{a_n}中，a₁=1，a_n-a_n-1=2（n≥2），則a₆=（　　）

  A．10

  B．11

  C．12

  D．13
  組卷：259引用：2難度：0.8

  解析

• 2．已知

  P

  （

  A

  ）

  =

  1

  2

  ，

  P

  （

  AB

  ）

  =

  1

  3

  ，那么P（B|A）=（　　）

  A． 1 6

  B． 1 3

  C． 2 3

  D． 5 6
  組卷：191引用：2難度：0.8

  解析

• 3．如圖所示的三角形圖案是謝爾賓斯基三角形．已知第n個圖案中黑色與白色三角形的個數之和為a_n，數列{a_n}滿足a₁=1，a_n+1=3a_n+1（n≥1），那么下面各數中是數列{a_n}中的項的是（　　）
  

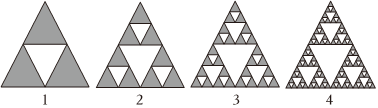
  A．121

  B．122

  C．123

  D．124
  組卷：161引用：3難度：0.5

  解析

• 4．已知某生物技術公司研制出一種新藥，并進行了臨床試驗，該臨床試驗的成功概率是失敗概率的2倍．若記一次試驗中成功的次數為X，則隨機變量X的數學期望為（　　）

  A． 2 3

  B． 1 2

  C． 1 3

  D． 1 6
  組卷：181引用：3難度：0.5

  解析

• 5．用充氣筒吹氣球，氣球會鼓起來，假設此時氣球是一個標準的球體，且氣球的體積V（r）隨著氣球半徑r的增大而增大．當半徑r=1時，氣球的體積

  V

  （

  r

  ）

  =

  4

  3

  π

  r

  3

  相對于r的瞬時變化率為（　　）

  A． 4 3 π

  B．2π

  C．4π

  D．8π
  組卷：197引用：5難度：0.7

  解析

• 6．某人需要先從A地到B地，再同站轉車趕到C地，他能夠選擇的高鐵車次的列車時刻表如下表所示，那么此人這天乘坐高鐵列車從A地到C地不同的乘車方案總數為（　　）
  A地至B地高鐵列車時刻表
  

  車次	發車時間	到站時間
  G87	07：00	08：01
  G91	07：55	08：56
  G93	09：00	10：01

  B地至C地高鐵列車時刻表

  車次	發車時間	到站時間
  G2811	08：25	10：31
  G653	09：24	11：13
  G501	10：26	12：30

  A．9

  B．6

  C．4

  D．3
  組卷：65引用：1難度：0.9

  解析

• 7．正態分布在概率和統計中占有重要地位，它廣泛存在于自然現象、生產和生活實踐之中．在現實生活中，很多隨機變量都服從或近似服從正態分布．假設隨機變量X～N（μ，σ²），可以證明，對給定的k∈N^*，P（μ-kσ≤X≤μ+kσ）是一個只與k有關的定值，部分結果如圖所示：
  通過對某次數學考試成績進行統計分析，發現考生的成績ξ基本服從正態分布ξ～N（105，10²）．若共有1000名考生參加這次考試，則考試成績在（105，125）的考生人數大約為（　　）

  A．341

  B．477

  C．498

  D．683
  組卷：178引用：2難度：0.7

  解析

三、解答題共6小題，共85分。解答應寫出文字說明，演算步驟或證明過程。

• 20．已知函數f（x）=e^x-ax-1（a∈R）．
  （1）求曲線y=f（x）在點（0，f（0））處的切線方程；
  （2）討論函數f（x）的單調性；
  （3）判斷e^0.01與1.01的大小關系，并說明理由．
  組卷：321引用：3難度：0.4

  解析

• 21．正實數構成的集合A={a₁，a₂，?，a_n}（n≥2），定義A?A={a_i?a_j|a_i，a_j∈A，且i≠j}．當集合A?A中的元素恰有

  n

  （

  n

  -

  1

  ）

  2

  個數時，稱集合A具有性質Ω．
  （Ⅰ）判斷集合A₁={1，2，4}，A₂={1，2，4，8}是否具有性質Ω；
  （Ⅱ）若集合A具有性質Ω，且A中所有元素能構成等比數列，A?A中所有元素也能構成等比數列，求集合A中的元素個數的最大值；
  （Ⅲ）若集合A具有性質Ω，且A?A中的所有元素能構成等比數列．問：集合A中的元素個數是否存在最大值？若存在，求出該最大值；若不存在，請說明理由．
  組卷：65引用：3難度：0.2

  解析