2022-2023學(xué)年江西省萍鄉(xiāng)市高二(下)期末數(shù)學(xué)試卷
發(fā)布:2024/6/13 8:0:9
一、單項(xiàng)選擇題:本大題共8小題,每小題5分,共40分.在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合題目要求的.
-
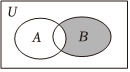 1.已知全集U=R,集合A={x|x≥2或x≤-3},B={x|0≤x≤4},則Venn圖中陰影部分表示的集合為( )
1.已知全集U=R,集合A={x|x≥2或x≤-3},B={x|0≤x≤4},則Venn圖中陰影部分表示的集合為( )A.[0,2) B.[0,3) C.(2,4] D.(3,4] 組卷:236引用:6難度:0.7 -
2.已知命題p:3x>1,命題q:x3>1,則p是q的( )
A.充分必要條件 B.充分不必要條件 C.必要不充分條件 D.既不充分也不必要條件 組卷:38引用:2難度:0.7 -
3.已知函數(shù)f(x)在x=x0處可導(dǎo),若
,則f′(x0)=( )△x→0limf(x0-4△x)-f(x0)△x=1A.1 B.-4 C. -14D.-1 組卷:52引用:3難度:0.8 -
4.已知a=0.20.3,b=log20.3,c=log0.30.2,則a,b,c的大小關(guān)系為( )
A.c>b>a B.c>a>b C.a(chǎn)>c>b D.a(chǎn)>b>c 組卷:128引用:1難度:0.8 -
5.已知函數(shù)f(x)及其導(dǎo)數(shù)f′(x),若存在x0使得f(x0)=f′(x0),則稱x0是f(x)的一個(gè)“巧值點(diǎn)”.下列四個(gè)函數(shù)中,沒有“巧值點(diǎn)”的是( )
A.f(x)=x2 B.f(x)=lnx C.f(x)=sinx D.f(x)=2x 組卷:126引用:3難度:0.7 -
6.唐代大詩人李白喜好飲酒作詩,民間有“李白斗酒詩百篇”之說.《算法統(tǒng)宗》中記載了一個(gè)“李白沽酒”的故事.詩云:今攜一壺酒,游春郊外走.逢朋加一倍,入店飲半斗.注:古代一斗是10升.大意是:李白在郊外春游時(shí),做出這樣一條約定:遇見朋友,先到酒店里將壺里的酒增加一倍(假定每次加酒不會(huì)溢出),再喝掉其中的5升酒.那么根據(jù)這個(gè)規(guī)則,若李白酒壺中原來有酒6升,將李白在第5家店飲酒后所剩酒量是( )
A.37升 B.21升 C.26升 D.32升 組卷:31引用:2難度:0.6 -
7.已知函數(shù)f(x)=lnx-(x-a)2(a∈R)在區(qū)間[1,+∞)上存在單調(diào)遞增區(qū)間,則實(shí)數(shù)a的取值范圍是( )
A. [12,+∞)B. (12,+∞)C.[1,+∞) D.(1,+∞) 組卷:285引用:4難度:0.6
四、解答題:本大題共6小題,共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.
-
21.已知函數(shù)
關(guān)于點(diǎn)f(x)=1+a4x+2對(duì)稱,其中a為實(shí)數(shù).(12,12)
(1)求實(shí)數(shù)a的值;
(2)若數(shù)列{an}的通項(xiàng)滿足,其前n項(xiàng)和為Sn,求S2022.an=f(n2023)組卷:62引用:1難度:0.5 -
22.已知函數(shù)
.f(x)=x22+cosx
(1)求函數(shù)f(x)的最小值;
(2)設(shè)函數(shù),試討論g(x)的單調(diào)性.g(x)=13x3-ax2+(x-2a)?cosx-sinx(a∈R)組卷:23引用:1難度:0.5


