當(dāng)前位置：試卷中心 > 試卷詳情

2023-2024學(xué)年福建省福州市鼓樓區(qū)格致中學(xué)高一（上）期中數(shù)學(xué)試卷（合格考）

發(fā)布：2024/10/8 9:0:1

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)符合題目要求.

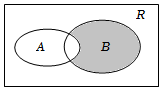1．設(shè)全集U=R，A={x|x-1≤0}，B={x|-1＜x＜2}，則圖中陰影部分對(duì)應(yīng)的集合為（　　）
A．A∩（?_RB） B．?_AB C．{x|1≤x＜2} D．{x|1＜x＜2}
組卷：132引用：4難度：0.7
解析
2．命題“?x＞1，x²-x＞0”的否定是（　　）
A．?x₀≤1，
x
0
2
-
x
0
≤
0
B．?x＞1，x²-x≤0
C．?x₀＞1，
x
0
2
-
x
0
≤
0
D．?x≤1，x²-x＞0
組卷：379引用：35難度：0.9
解析
3．函數(shù)f（x）=ax²+（2+a）x+1是偶函數(shù)，則函數(shù)的單調(diào)遞增區(qū)間為（　　）
A．[0，+∞） B．（-∞，0] C．（-∞，+∞） D．[1，+∞）
組卷：348引用：8難度：0.9
解析
4．若非零實(shí)數(shù)a,b滿足|a|＞|b|，則下列不等式中一定成立的是（　　）
A．a(chǎn)-b＞0 B．a(chǎn)²-b²＞0 C．a(chǎn)³-b³＞0 D．
1
a
＜
1
b
組卷：171引用：8難度：0.7
解析
5．已知函數(shù)
f
（
x
）
=
x
2
-
2
ax
,
x
≥
1
ax
-
1
，
x
＜
1
是R上的增函數(shù)，則實(shí)數(shù)a的取值范圍是（　　）
A．（0，
2
3
） B．（0，
2
3
] C．（0，1） D．（0，1]
組卷：281引用：9難度：0.7
解析
6．已知關(guān)于x的不等式ax²+bx+c＜0的解集是（-∞，-2）∪（1，+∞），則不等式
ax
+
b
bx
+
c
＞
0
的解集是（　　）
A．（-∞，-2）∪（1，+∞） B．（-2，1）
C．（-∞，-1）∪（2，+∞） D．（-1，2）
組卷：114引用：3難度：0.7
解析
7．若定義在R的奇函數(shù)f（x）在（-∞，0）單調(diào)遞減，且f（2）=0，則滿足xf（x-1）≥0的x的取值范圍是（　　）
A．[-1，1]∪[3，+∞） B．[-3，-1]∪[0，1] C．[-1，0]∪[1，+∞） D．[-1，0]∪[1，3]
組卷：754引用：82難度：0.6
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部?jī)?nèi)容及下載

四、解答題：本題共6題，共70分，解答應(yīng)寫(xiě)出文字說(shuō)明，證明過(guò)程或演算步驟.

21．已知函數(shù)
f
（
x
）
=
x
+
k
x
，x∈（0，+∞）有如下性質(zhì)：如果常數(shù)k＞0，那么該函數(shù)在
（
0
，
k
]
上是減函數(shù)，在
[
k
，
+
∞
）
上是增函數(shù)．
（1）請(qǐng)任選函數(shù)兩個(gè)單調(diào)區(qū)間中的一個(gè)，證明上述結(jié)論；
（2）利用上述性質(zhì)或用其它方法解決下列問(wèn)題：
①若a＞0，函數(shù)
y
=
x
+
a
x
（
x
＞
0
）
的值域?yàn)閇6，+∞），求實(shí)數(shù)a的值；
②若關(guān)于x的方程4x²-2（b+6）x-b-3=0在x∈[0，1]上有解，求實(shí)數(shù)b的取值范圍．
組卷：18引用：2難度：0.4
解析
22．對(duì)于函數(shù)f（x），若存在x∈R，使f（x₀）=x₀成立，則稱(chēng)x₀為f（x）的不動(dòng)點(diǎn)．已知函數(shù)f（x）=ax²+（b+1）x+（b-1）（a≠0）．
（1）當(dāng)a=1，b=3時(shí)，求函數(shù)f（x）的不動(dòng)點(diǎn)；
（2）若對(duì)任意實(shí)數(shù)b,函數(shù)f（x）恒有兩個(gè)相異的不動(dòng)點(diǎn)，求a的取值范圍；
（3）在（2）的條件下，若f（x）的兩個(gè)不動(dòng)點(diǎn)為x₁，x₂，且
f
（
x
1
）
+
x
2
=
-
1
2
a
2
+
1
，求實(shí)數(shù)b的取值范圍．
組卷：105引用：7難度：0.5
解析