2022-2023學年廣東省東莞市松山湖橫瀝實驗學校八年級(上)期中數學試卷
發布:2024/10/25 3:0:4
一、選擇題(本題共10小題,每小題3分,共30分。每小題只有一個選項符合題意)
-
1.下列圖形是軸對稱圖形的是( )
A. 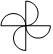
B. 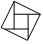
C. 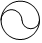
D. 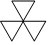 組卷:109引用:7難度:0.9
組卷:109引用:7難度:0.9 -
2.在下列長度的各組線段中,能組成三角形的是( )
A.5,5,10 B.1,4,9 C.5,12,6 D.3,4,5 組卷:74引用:9難度:0.9 -
3.下列圖形中具有穩定性的是( )
A.平行四邊形 B.等腰三角形 C.長方形 D.梯形 組卷:909引用:7難度:0.9 -
4.如圖,∠ACD=120°,∠B=20°,則∠A的度數是( )
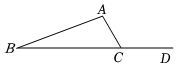
A.120° B.90° C.100° D.30° 組卷:702引用:16難度:0.7 -
5.如果一個正多邊形內角和等于1080°,那么這個正多邊形的每一個外角等于( )
A.45° B.60° C.120° D.135° 組卷:1329引用:11難度:0.9 -
6.已知等腰三角形的一邊長為2cm,另一邊長為4cm,則它周長是( )
A.6cm B.8cm C.10cm D.8cm或10cm 組卷:366引用:5難度:0.5 -
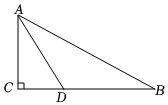 7.如圖,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于點D,若BC=12,BD=8,則點D到AB的距離是( )
7.如圖,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于點D,若BC=12,BD=8,則點D到AB的距離是( )A.2 B.6 C.4 D.8 組卷:19引用:1難度:0.5 -
8.下列計算正確的是( )
A.a3?a2=a6 B.(m+2)2=m2+4 C.b6÷b3=b2 D.(-x2y)3=-x6y3 組卷:28引用:2難度:0.8
四.解答題(每題8分,共40分)
-
24.已知AB=4cm,AC=BD=3cm.點P在AB上以1cm/s的速度由點A向點B運動,同時點Q在BD上由點B向點D運動.它們運動的時間為t(s).

(1)如圖①,AC⊥AB,BD⊥AB,若點Q的運動速度與點P的運動速度相等,當t=1時,△ACP與△BPQ是否全等,請說明理由,并判斷此時線段PC和線段PQ的位置關系;
(2)如圖②,將圖①中的“AC⊥AB,BD⊥AB”為改“∠CAB=∠DBA=60°”,其他條件不變.設點Q的運動速度為x cm/s,是否存在實數x,使得△ACP與△BPQ全等?若存在,求出相應的x、t的值;若不存在,請說明理由.組卷:422引用:1難度:0.6 -
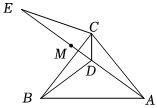 25.如圖,在△ABC中,AC=BC,∠ACB=90°,點D為△ABC內一點,且BD=AD.
25.如圖,在△ABC中,AC=BC,∠ACB=90°,點D為△ABC內一點,且BD=AD.
(1)求證:CD⊥AB;
(2)∠CAD=15°,E為延長線上的一點,且CE=CA.
①求證:DE平分∠BDC;
②若點AM在DE上,且DC=DM,請判斷ME、BD的數量關系,并給出證明.組卷:311引用:8難度:0.5


