當前位置：試卷中心 > 試卷詳情

2023-2024學年北京市懷柔一中高二（上）開學數學試卷

發布：2024/8/3 8:0:9

一、選擇題

1．已知
a
=（1，2），
b
=（4，-2），下列說法正確的是（　　）
A．
|
a
|
=
3
B．
a
⊥
b
C．
a
∥
b
D．
b
-
a
=
（
3
，
4
）
組卷：150引用：4難度：0.8
解析
2．扇子具有悠久的歷史，蘊含著豐富的數學元素．小明制作了一把如圖所示的扇子，其半徑為16cm,圓心角為135°，則這把扇子的弧長為（　　）
A．6πcm B．12πcm C．18πcm D．24πcm
組卷：219引用：1難度：0.7
解析
3．已知
cosα
=
-
5
5
，α∈
（
π
2
，
π
）
，則
tan
（
π
4
+
α
）
=（　　）
A．
1
3
B．3 C．-3 D．
-
1
3
組卷：282引用：3難度：0.8
解析
4．下列函數中，最小正周期為π且是偶函數的是（　　）
A．
y
=
sin
（
x
+
π
2
）
B．y=tanx
C．y=cos2x D．y=sin2x
組卷：42引用：1難度：0.7
解析
5．在平行四邊形ABCD中，M是DC的中點，向量
DN
=
2
NB
，設
AB
=
a
，
AD
=
b
，則
MN
=（　　）
A．
1
6
a
-
2
3
b
B．-
1
6
a
+
1
3
b
C．
1
6
a
+
7
6
b
D．
1
6
a
-
1
3
b
組卷：634引用：4難度：0.8
解析
6．將函數y=sin（2x）的圖象沿x軸向右平移φ（φ＞0）個單位長度，得到函數
y
=
sin
（
2
x
-
π
3
）
的圖象，則φ的最小值為（　　）
A．
φ
=
π
6
B．
φ
=
π
3
C．
φ
=
2
π
3
D．
φ
=
5
π
6
組卷：159引用：2難度：0.6
解析
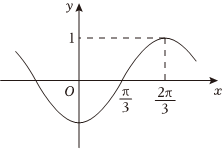7．已知函數f（x）=sin（ωx+φ）（ω＞0、|φ|＜π）的部分圖象如圖所示，則
f
（
π
6
）
=（　　）
A．
3
2
B．-
2
2
C．0 D．
2
2
組卷：679引用：5難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題

20．在△ABC中，角A，B，C的對邊分別為a,b,c,已知
cos
A
=
-
1
4
，
b
=
4
．
（1）當
a
=
2
6
時，求△ABC的面積；
（2）再從下列三個條件中選擇一個作為已知，使得三角形存在且唯一確定，并求a的值．
條件①：acosA=bcosB；
條件②：
2
sin
2
C
=
6
cos
C
；
條件③：
3
a
=
bsin
C
+
3
bcos
C
．
組卷：120引用：4難度：0.5
解析
21．如圖，在四棱錐S-ABCD中，平面SAD⊥平面ABCD，SA=SD=AD=2，四邊形ABCD為正方形，E為AD的中點，F為SB上一點，M為BC上一點，且平面EFM∥平面SCD．
（1）求證：M為線段BC中點；
（2）求證：平面SAD⊥平面SCD；
（3）在棱SC上是否存在點N，使得平面DMN⊥平面ABCD？若存在，求
CN
CS
；若不存在，說明理由．
組卷：142引用：2難度：0.5
解析