當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東實驗中學（深圳學校）高一（下）期中數學試卷

發布：2024/4/20 14:35:0

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．已知復數z滿足（-3i）z=4-5i,則z的虛部為（　　）
A．
4
i
3
B．
4
3
C．
-
4
3
D．
-
4
i
3
組卷：76引用：3難度：0.8
解析
2．平面向量
a
=（-2，k），
b
=（2，4），若
a
⊥
b
，則|
a
-
b
|=（　　）
A．6 B．5 C．
2
6
D．
2
5
組卷：786引用：5難度：0.9
解析
3．在△ABC中，若（a+b+c）（c+b-a）=bc,則A=（　　）
A．
5
π
6
B．
2
π
3
C．
π
3
D．
π
6
組卷：546引用：4難度：0.8
解析
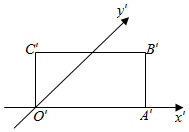4．如圖，矩形OABC′是水平放置的一個平面圖形的直觀圖，其中OA′=6，OC′=2，則原圖形OABC的面積為（　　）
A．24
2
B．12
2
C．48
2
D．20
2
組卷：426引用：15難度：0.9
解析
5．在如圖所示的半圓中，AB為直徑，點O為圓心，C為半圓上一點，且∠OCB=30°，
|
AB
|
=
2
，則
|
AC
|
等于（　　）
A．1 B．
2
C．
3
D．2
組卷：193引用：6難度：0.8
解析
6．若圓錐高為3，體積為3π，則該圓錐的側面積為（　　）
A．4π B．5π C．6π D．7π
組卷：275引用：4難度：0.8
解析
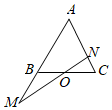7．如圖所示，在△ABC中，點O是BC的中點，過點O的直線分別交直線AB、AC于不同的兩點M、N，若
AB
=m
AM
，
AC
=n
AN
（m,n＞0），則
1
m
+
4
n
的最小值為（　　）
A．2 B．3 C．
9
2
D．5
組卷：615引用：9難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

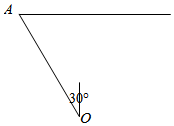21．某港口O要將一件重要物品用小艇送到一艘正在航行的輪船上，在小艇出發時，輪船位于港口O北偏西30°且與該港口相距20海里的A處，并正以30海里/小時的航行速度沿正東方向勻速行駛．假設該小艇沿直線方向以v海里/小時的航行速度勻速行駛，經過t小時與輪船相遇．
（Ⅰ）若希望相遇時小艇的航行距離最小，則小艇航行速度的大小應為多少？
（Ⅱ）為保證小艇在30分鐘內（含30分鐘）能與輪船相遇，試確定小艇航行速度的最小值．
組卷：165引用：13難度：0.7
解析
22．在平面直角坐標系中，O為坐標原點，對任意兩個向量
m
=（x₁，y₁），
n
=（x₂，y₂），作：
OM
=
m
，
ON
=
n
．當
m
，
n
不共線時，記以OM，ON為鄰邊的平行四邊形的面積為S（
m
，
n
）=|x₁y₂-x₂y₁|；當
m
，
n
共線時，規定S（
m
，
n
）=0．
（Ⅰ）分別根據下列已知條件求S（
m
，
n
）：
①
m
=（2，1），
n
=（-1，2）；②
m
=（1，2），
n
=（2，4）；
（Ⅱ）若向量
p
=λ
m
+μ
n
（λ，μ∈R，λ²+μ²≠0），
求證：S（
p
，
m
）+S（
p
，
n
）=（|λ|+|μ|）S（
m
，
n
）；
（Ⅲ）若A，B，C是以O為圓心的單位圓上不同的點，記
OA
=
a
，
OB
=
b
，
OC
=
c
．
（ⅰ）當
a
⊥
b
時，求S（
c
，
a
）+S（
c
，
b
）的最大值；
（ⅱ）寫出S（
a
，
b
）+S（
b
，
c
）+S（
c
，
a
）的最大值．（只需寫出結果）
組卷：360引用：8難度：0.3
解析