2022-2023學(xué)年江蘇省揚州市江都區(qū)邵樊片八年級（下）第二次月考數(shù)學(xué)試卷

一、選擇題（每題3分，共24分）

• 1．下列圖形中既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．

  B．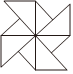

  C．

  D．
  組卷：52引用：2難度：0.9

  解析

• 2．下列調(diào)查適合普查的是（　　）

  A．夏季冷飲市場上冰淇淋的質(zhì)量

  B．2023年初三學(xué)生的體育中考成績

  C．江都區(qū)初中生的視力情況

  D．某批燈泡的使用壽命
  組卷：44引用：2難度：0.7

  解析

• 3．下列事件是隨機事件的是（　　）

  A．沒有水分，種子發(fā)芽

  B．367人中至少有2人的生日相同

  C．在標(biāo)準氣壓下，-1℃冰熔化

  D．小明買了一張彩票中獎
  組卷：33引用：2難度：0.9

  解析

• 4．下列運算正確的是（　　）

  A． a 2 - b 2 （ a - b ） 2 = a + b a - b	B． a 2 - b 2 a 2 + b 2 = a - b a + b
  C． x - 1 1 - x 2 = 1 x + 1	D． - x - y - x + y = x - y x + y
  組卷：392引用：2難度：0.9

  解析

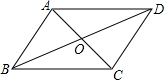• 5．如圖，在四邊形ABCD中，對角線AC、BD相交于點O．下列條件不能判定四邊形ABCD為平行四邊形的是（　　）

  A．AB∥CD，AD∥BC	B．OA=OC，OB=OD
  C．AB=CD，AD=BC	D．AB∥CD，AD=BC
  組卷：650引用：12難度：0.9

  解析

• 6．若A（x₁，y₁），B（x₂，y₂），C（x₃，y₃）是反比例函數(shù)y=

  3

  x

  圖象上的點，且x₁＜x₂＜0＜x₃，則y₁、y₂、y₃的大小關(guān)系正確的是（　　）

  A．y3＞y1＞y2

  B．y1＞y2＞y3

  C．y2＞y1＞y3

  D．y3＞y2＞y1
  組卷：329引用：18難度：0.9

  解析

• 7．函數(shù)

  y

  =

  2

  |

  x

  |

  的圖象是（　　）

  A．

  B．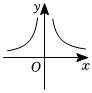

  C．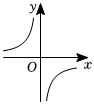

  D．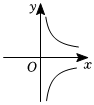
  組卷：323引用：5難度：0.7

  解析

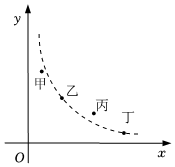• 8．某市舉行中學(xué)生黨史知識競賽，如圖用四個點分別描述甲、乙、丙、丁四所學(xué)校競賽成績的優(yōu)秀率（該校優(yōu)秀人數(shù)與該校參加競賽人數(shù)的比值）y與該校參加競賽人數(shù)x的情況，其中描述乙、丁兩所學(xué)校情況的點恰好在同一個反比例函數(shù)的圖象上，則這四所學(xué)校在這次黨史知識競賽中成績優(yōu)秀人數(shù)最多的是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  組卷：1764引用：13難度：0.7

  解析

二、填空題（每題3分，共30分）

• 9．若

  y

  =

  （

  a

  +

  1

  ）

  x

  a

  2

  -

  2

  是反比例函數(shù)，則a的取值為

  ．
  組卷：554引用：8難度：0.9

  解析

三、解答題（共96分）

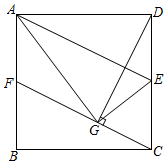• 27．如圖，四邊形ABCD為正方形，點E、F分別是CD、AB的中點，DG⊥CF于點G．
  （1）求證：AE∥CF；
  （2）求證：∠AGE=90°；
  （3）若正方形的邊長為2，則線段CG的長度為

  ．
  組卷：945引用：2難度：0.6

  解析

• 28．在平面直角坐標(biāo)系xOy中，對于任意三點A，B，C的“矩面積”，給出如下定義：
  “水平底”a：任意兩點橫坐標(biāo)差的最大值，“鉛垂高”h：任意兩點縱坐標(biāo)差的最大值，則“矩面積”S=ah.
  例如：三點坐標(biāo)分別為A（1，2），B（-3，1），C（2，-2），則“水平底”a=5，“鉛垂高”h=4，“矩面積”S=ah=20．
  （1）已知點A（1，2），B（-3，1），P（0，t）．
  ①若A，B，P三點的“矩面積”為12，求點P的坐標(biāo)；
  ②直接寫出A，B，P三點的“矩面積”的最小值．
  （2）已知點E（4，0），F(xiàn)（0，2），M（m,4m），N（n,

  16

  n

  ），其中m＞0，n＞0．
  ①若E，F(xiàn)，M三點的“矩面積”為8，求m的取值范圍；
  ②直接寫出E，F(xiàn)，N三點的“矩面積”的最小值及對應(yīng)n的取值范圍．
  組卷：934引用：5難度：0.1

  解析