人教五四新版九年級（上）中考題單元試卷：第30章 旋轉(zhuǎn)（03）
發(fā)布：2024/4/20 14:35:0
一、選擇題（共12小題）
-
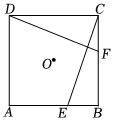1．如圖，E、F分別是正方形ABCD的邊AB、BC上的點(diǎn)，BE=CF，連接CE、DF．將△BCE繞著正方形的中心O按逆時針方向旋轉(zhuǎn)到△CDF的位置，則旋轉(zhuǎn)角是（ ）組卷：1002引用：69難度：0.9 -
2．如圖，點(diǎn)A、B、C、D都在方格紙的格點(diǎn)上，若△AOB繞點(diǎn)O按逆時針方向旋轉(zhuǎn)到△COD的位置，則旋轉(zhuǎn)的角度為（ ）組卷：960引用：85難度：0.9 -
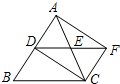3．如圖，在△ABC中，AC=BC，點(diǎn)D、E分別是邊AB、AC的中點(diǎn)，將△ADE繞點(diǎn)E旋轉(zhuǎn)180°得△CFE，則四邊形ADCF一定是（ ）組卷：1013引用：94難度：0.9 -
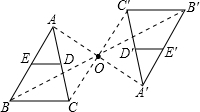4．如圖，△ABC以點(diǎn)O為旋轉(zhuǎn)中心，旋轉(zhuǎn)180°后得到△A′B′C′．ED是△ABC的中位線，經(jīng)旋轉(zhuǎn)后為線段E′D′．已知BC=4，則E′D′=（ ）組卷：512引用：66難度：0.9 -
5．如圖，在Rt△ABC中，∠ACB=90°，∠ABC=30°，將△ABC繞點(diǎn)C順時針旋轉(zhuǎn)至△A′B′C，使得點(diǎn)A′恰好落在AB上，則旋轉(zhuǎn)角度為（ ）組卷：2880引用：90難度：0.9 -
6．如圖，Rt△ABC中，∠ACB=90°，AC=BC=2，在以AB的中點(diǎn)O為坐標(biāo)原點(diǎn)，AB所在直線為x軸建立的平面直角坐標(biāo)系中，將△ABC繞點(diǎn)B順時針旋轉(zhuǎn)，使點(diǎn)A旋轉(zhuǎn)至y軸正半軸上的A′處，則圖中陰影部分面積為（ ）組卷：1808引用：63難度：0.5 -
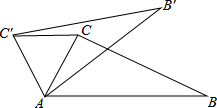7．如圖，在△ABC中，∠CAB=70°，將△ABC繞點(diǎn)A逆時針旋轉(zhuǎn)到△AB′C′的位置，使得CC′∥AB，則∠BAB′的度數(shù)是（ ）組卷：2479引用：89難度：0.7 -
8．如圖，△ABC中，∠CAB=65°，在同一平面內(nèi)，將△ABC繞點(diǎn)A旋轉(zhuǎn)到△AED的位置，使得DC∥AB，則∠BAE等于（ ）組卷：1933引用：91難度：0.9 -
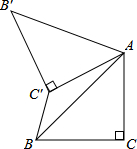9．如圖，已知△ABC中，∠C=90°，AC=BC=，將△ABC繞點(diǎn)A順時針方向旋轉(zhuǎn)60°到△AB′C′的位置，連接C′B，則C′B的長為（ ）2組卷：12118引用：96難度：0.5 -
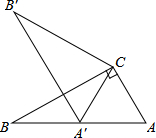
10．如圖，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC繞點(diǎn)C順時針旋轉(zhuǎn)得到，其中點(diǎn)A′與點(diǎn)A是對應(yīng)點(diǎn)，點(diǎn)B′與點(diǎn)B是對應(yīng)點(diǎn)，連接AB′，且A、B′、A′在同一條直線上，則AA′的長為（ ）組卷：185引用：74難度：0.6
三、解答題（共5小題）
-
29．已知△ABC中，M為BC的中點(diǎn)，直線m繞點(diǎn)A旋轉(zhuǎn)，過B、M、C分別作BD⊥m于D，ME⊥m于E，CF⊥m于F．
（1）當(dāng)直線m經(jīng)過B點(diǎn)時，如圖1，易證EM=CF．（不需證明）12
（2）當(dāng)直線m不經(jīng)過B點(diǎn)，旋轉(zhuǎn)到如圖2、圖3的位置時，線段BD、ME、CF之間有怎樣的數(shù)量關(guān)系？請直接寫出你的猜想，并選擇一種情況加以證明．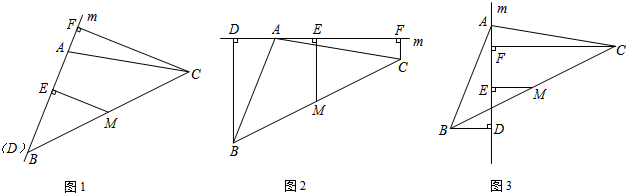
組卷：1822引用：56難度：0.3 -
30．兩個長為2cm,寬為1cm的長方形，擺放在直線l上（如圖①），CE=2cm,將長方形ABCD繞著點(diǎn)C順時針旋轉(zhuǎn)α角，將長方形EFGH繞著點(diǎn)E逆時針旋轉(zhuǎn)相同的角度．
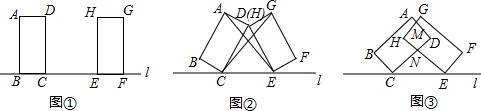
（1）當(dāng)旋轉(zhuǎn)到頂點(diǎn)D、H重合時，連接AE、CG，求證：△AED≌△GCD（如圖②）．
（2）當(dāng)α=45°時（如圖③），求證：四邊形MHND為正方形．組卷：852引用：57難度：0.3