2022-2023學年北京理工大學附中高三（上）月考數學試卷（10月份）

一、選擇題：共10小題，每小題4分，共40分，在每小題列出的四個選項中，選出符合題目要求的一項。

• 1．若集合M={x||x|≤2}，N={x|x²-3x=0}，則M∩N等于（　　）

  A．{3}

  B．{0}

  C．{0，2}

  D．{0，3}
  組卷：300引用：14難度：0.9

  解析

• 2．在復平面內，復數z=i（2+i）對應的點的坐標為（　　）

  A．（1，2）

  B．（-1，2）

  C．（2，1）

  D．（2，-1）
  組卷：116引用：8難度：0.8

  解析

• 3．已知

  α

  ∈

  （

  π

  2

  ，

  3

  π

  2

  ）

  ，且

  tanα

  =

  2

  ，那么sinα=（　　）

  A． - 3 3

  B． - 6 3

  C． 6 3

  D． 3 3
  組卷：329引用：10難度：0.8

  解析

• 4．函數y=sin（x+φ）的圖象關于y軸對稱的充分必要條件是（　　）

  A．φ= π 2	B．φ=π
  C．φ=kπ+ π 2 ，k∈Z	D．φ=2kπ+ π 2 ，k∈Z
  組卷：133引用：2難度：0.7

  解析

• 5．函數y=2^x+

  2

  2

  x

  的最小值為（　　）

  A．1

  B．2

  C．2 2

  D．4
  組卷：118引用：4難度：0.9

  解析

• 6．在同一個坐標系中畫出函數y=a^x，y=sinax的部分圖象，其中a＞0且a≠1，則下列所給圖象中可能正確的是（　　）

  A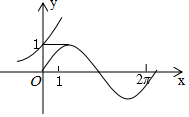．	B．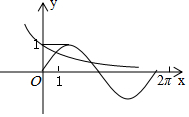
  C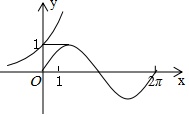．	D．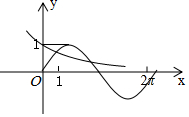
  組卷：4521引用：46難度：0.7

  解析

• 7．已知x₁=

  log

  1

  3

  2，x₂=

  2

  -

  1

  2

  ，x₃滿足（

  1

  3

  ）

  x

  3

  =log₃x₃，則（　　）

  A．x1＜x3＜x2

  B．x1＜x2＜x3

  C．x2＜x1＜x3

  D．x3＜x1＜x2
  組卷：472引用：14難度：0.9

  解析

三、解答題共6小題，共85分，解答應寫出文字說明，演算步驟或證明過程.

• 20．設函數f（x）=lnx-ax；g（x）=e^x-ax,其中a為實數．
  （1）若a=1，求f（x）的極值和單調區間；
  （2）若g（x）在（1，+∞）上有最小值，求a的取值范圍；
  （3）若g（x）在（-1，+∞）上是單調增函數，試求f（x）的零點個數，并證明你的結論．
  組卷：119引用：1難度：0.2

  解析

• 21．對于數列A：a₁，a₂，…，a_n（n≥3），定義變換T，T將數列A變換成數列T（A）：a₂，a₃，…，a_n，a₁，記T¹（A）=T（A），T^m（A）=T（T^m-1（A）），m≥2．
  對于數列A：a₁，a₂，…，a_n與B：b₁，b₂，…，b_n，定義A?B=a₁b₁+a₂b₂+…+a_nb_n．
  若數列A：a₁，a₂，…，a_n（n≥3）滿足a_i∈{-1，1}（i=1，2，…，n），則稱數列A為?_n數列．
  （1）若A：-1，-1，1，-1，1，1，寫出T（A），并求A?T²（A）；
  （2）對于任意給定的正整數n（n≥3），是否存在?_n數列A，使得A?T（A）=n-3？若存在，寫出一個數列A，若不存在，說明理由；
  （3）若?_n數列A滿足T^k（A）?T^k+1（A）=n-4（k=1，2，…，n-2），求數列A的個數．
  組卷：309引用：9難度：0.5

  解析