2023年江蘇省連云港市海州區新海實驗中學中考數學二模試卷

一、選擇題（本大題共有8小題，每小題3分，共24分.在每小題給出的四個選項中，只有一項是符合題目要求的，請將正確選項前的字母代號填涂在答題卡相應位置上.）

• 1．-2的倒數是（　　）

  A．-2

  B．- 1 2

  C． 1 2

  D．2
  組卷：3978引用：688難度：0.9

  解析

• 2．下列運算正確的是（　　）

  A．3a+2b=5ab	B．5a2-2a2=3
  C．7a+a=7a2	D．（x-1）2=x2+1-2x
  組卷：107引用：5難度：0.8

  解析

• 3．第十二屆江蘇省園藝博覽會以“山海連云，絲路綠韻”為主題，耗資約20.8億打造的連云港園博園于2023年4月26日盛大開園．把數字“20.8億”用科學記數法表示為（　　）

  A．2.08×108

  B．2.08×109

  C．0.208×1010

  D．20.8×108
  組卷：45引用：2難度：0.7

  解析

• 4．如圖，由3個大小相同的正方體搭成的幾何體，其主視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：108引用：71難度：0.9

  解析

• 5．下列說法正確的是（　　）

  A．為了解我國中小學生的睡眠情況，應采取全面調查的方式

  B．一組數據1，2，5，5，5，3，3的眾數和平均數都是3

  C．若甲、乙兩組數據的方差分別是0.01，0.1，則甲組數據比乙組數據更穩定

  D．拋擲一枚硬幣200次，一定有100次“正面向上”
  組卷：451引用：12難度：0.7

  解析

• 6．A、B兩地相距80千米，一輛大汽車從A地開出2小時后，又從A地開出另一輛小汽車，已知小汽車的速度是大汽車速度的3倍，結果小汽車比大汽車早40分鐘到達B地，求兩種汽車每小時各走多少千米．設大汽車的速度為xkm/h,則下面所列方程正確的是（　　）

  A． 80 x - 80 3 x =40	B． 80 x - 80 3 x =2.4
  C． 80 x -2= 80 3 x + 2 3	D． 80 x +2= 80 3 x - 2 3
  組卷：329引用：4難度：0.9

  解析

• 7．如圖，A，B，C是⊙O上三點，∠ACB=25°，則∠BAO的度數是（　　）

  A．55°

  B．60°

  C．65°

  D．70°
  組卷：5945引用：81難度：0.9

  解析

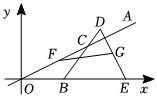• 8．如圖，在平面直角坐標系中，點

  E

  （

  4

  5

  ，0），點B是線段OE上任意一點，在射線
  OA上取一點C，使OB=BC，在射線BC上取一點D，使BD=BE．OA所在直線的關系式為

  y

  =

  1

  2

  x

  ，點F、G分別為線段OC、DE的中點，則FG的最小值是（　　）

  A． 8 5 5

  B． 4 5 5

  C． 2 5

  D．4.8
  組卷：118引用：1難度：0.6

  解析

二、填空題（本大題共有8小題，每小題3分，共24分.不需要寫出解答過程，請把答案

• 9．函數y=

  1

  x

  -

  2

  中自變量x的取值范圍是

  ．
  組卷：322引用：14難度：0.8

  解析

三、解答題（本大題共11小題，共102分.請在答題卡上指定區域內作答.解答時寫出必要的文字說明、證明過程或演算步驟.）

• 26．如圖①，動點P從矩形ABCD的頂點A出發，以v₁的速度沿折線A-B-C向終點C運動；同時，一動點Q從點D出發，以v₂的速度沿DC向終點C運動，當一個點到達終點時，另一個點也停止運動．點E為CD的中點，連接PE，PQ，記△EPQ的面積為S，點P運動的時間為t,其函數圖象為折線MN-NF和曲線FG（圖②），已知，ON=4，NH=1，點G的坐標為（8，0）．
  （1）點P與點Q的速度之比

  v

  1

  v

  2

  的值為

  ；

  AB

  AD

  的值為

  ；
  （2）如果OM=15．
  ①求線段NF所在直線的函數表達式；
  ②求FG所在曲線的函數表達式；
  ③是否存在某個時刻t,使得

  S

  ≥

  15

  4

  ？若存在，求出t的取值范圍：若不存在，請說明理由．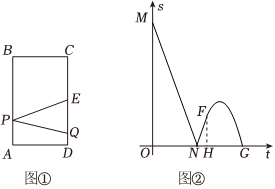
  
  組卷：537引用：7難度：0.2

  解析

• 27．問題提出：
  （1）在學習幾何時，我們可以通過構造基本圖形，將幾何“模型“化．例如在三角形全等與三角形的相似的學習過程中，“k”字形是非常重要的基本圖形．如圖1，已知：∠ADC=∠BEC=∠ACB=90°，D、C、E三點共線，AC=BC，由ASA易證△ADC≌△CEB；
  如圖2，已知：∠ADC=∠BEC=∠ACB=90°，D、C、E三點共線，若AC=6、BC=3、BE=1，則AD的長為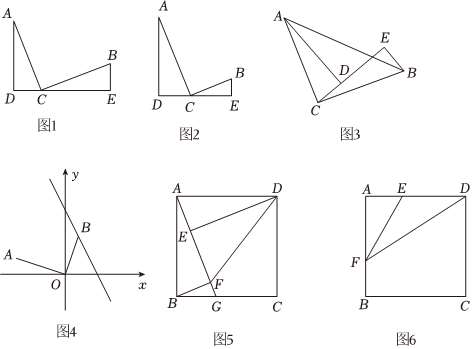

  ；
  
  問題探究：
  （2）①如圖3，已知：∠ADC=∠BEC=∠ACB=90°，AC=BC，D、C、E三點共線，求證：AD=BE+DE；
  ②如圖4，已知點A（-3，1），點B在直線y=-2x+4上，若∠AOB=90°，則此時點B的坐標為

  ；
  問題拓展：
  （3）如圖5，正方形ABCD中，點G是BC邊上一點，BF⊥AG，DE⊥AG，垂足分別為F、E．若AE=1，四邊形ABFD的面積等于10，求正方形ABCD的面積．
  （4）如圖6，正方形ABCD中，點E、F分別在AD、AB邊上，AE=BF，連接EF、DF，則

  EF

  DF

  的最小值是

  ．
  組卷：329引用：1難度：0.1

  解析