2022-2023學年四川省成都市青羊區石室中學高二（下）零診數學試卷（文科）

一、選擇題（本題共12道小題，每小題5分，共60分）

• 1．若復數z=a+bi（a,b∈R）滿足

  2

  z

  +

  z

  =

  3

  -

  i

  ，其中i為虛數單位，則|z|=（　　）

  A． 2

  B． 3

  C．2

  D．3
  組卷：34引用：2難度：0.8

  解析

• 2．在某校高中籃球聯賽中，某班甲、乙兩名籃球運動員在8場比賽中的單場得分用莖葉圖表示（如圖一），莖葉圖中甲的得分有部分數據丟失，但甲得分的折線圖（如圖二）完好，則下列結論正確的是（　　）
  

  A．甲得分的極差是18

  B．乙得分的中位數是16.5

  C．甲得分更穩定

  D．甲的單場平均得分比乙低
  組卷：139引用：9難度：0.8

  解析

• 3．某老師為了了解數學學習成績得分y（單位：分）與每天數學學習時間x（單位：分鐘）是否存在線性關系，搜集了100組數據

  100

  ∑

  i

  =

  1

  x

  i

  =

  5600

  ，

  100

  ∑

  i

  =

  1

  y

  i

  =

  11200

  ，并據此求得y關于x的線性回歸方程為

  ?

  y

  =

  ?

  b

  x+56??．若一位同學每天數學學習時間約80分鐘，則可估計這位同學數學成績為（　　）

  A．106

  B．122

  C．136

  D．140
  組卷：49引用：3難度：0.5

  解析

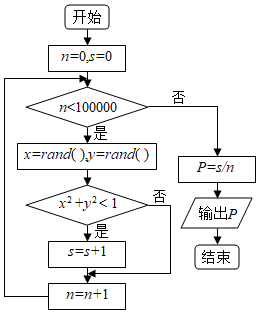• 4．利用隨機模擬方法可估計無理數π的數值，為此設計如圖所示的程序框圖，其中rand（　　）表示產生區間（0，1）上的隨機數，P是s與n的比值，執行此程序框圖，輸出結果P的值趨近于（　　）

  A．π

  B． π 4

  C． π 2

  D． 2 2 π
  組卷：6引用：4難度：0.7

  解析

• 5．已知命題p：k＜1，命題q：直線kx-y+1=0與拋物線y²=4x有兩個公共點，則p是q的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：63引用：4難度：0.5

  解析

• 6．有6名選手參加演講比賽，觀眾甲猜測：4號或5號選手得第一名；觀眾乙猜測：3號選手不可能得第一名；觀眾丙猜測：1，2，6號選手中的一位獲得第一名；觀眾丁猜測：4，5，6號選手都不可能獲得第一名．比賽后發現沒有并列名次，且甲、乙、丙、丁中只有1人猜對比賽結果，此人是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  組卷：229引用：12難度：0.7

  解析

• 7．已知函數f（x）=

  1

  ln

  （

  x

  +

  1

  ）

  -

  x

  ，則y=f（x）的圖象大致為（　　）

  A．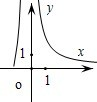

  B．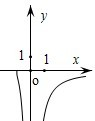

  C．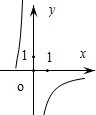

  D．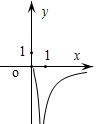
  組卷：4032引用：39難度：0.9

  解析

三、解答題（本題共6道小題，22題10分，其余各題12分，共70分）

• 21．已知函數f（x）=xlnx-a（x-1）．
  （1）若f（x）≥0，求實數a的值；
  （2）已知n∈N^*且n≥2，求證：

  sin

  1

  2

  +

  sin

  1

  3

  +

  ?

  +

  sin

  1

  n

  ＜

  lnn

  ．
  組卷：121引用：3難度：0.4

  解析

• 22．在直角坐標系xOy中，直線l₁的參數方程為

  x = 1 - m

  y = k （ m - 1 ）

  （m為參數），直線l₂的參數方程

  x = n

  y = 2 + n k

  （n為參數）．若直線l₁，l₂的交點為P，當k變化時，點P的軌跡是曲線C．
  （1）求曲線C的普通方程；
  （2）以坐標原點為極點，x軸正半軸為極軸且取相同的單位長度建立極坐標系，點A，B是曲線C兩動點，∠AOB=60°，求△AOB面積的最大值．
  組卷：27引用：3難度：0.5

  解析