當前位置：試卷中心 > 試卷詳情

2022-2023學年山西省大同市陽高四中高二（下）期末數學試卷

發布：2024/6/3 8:0:1

一、選擇題（本大題共12道小題，每小題5分，共計60分。在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．i為虛數單位，則
i
2
i
4
+
i
=（　　）
A．
-
1
-
i
2
B．
-
1
+
i
2
C．
1
+
i
2
D．
1
-
i
2
組卷：80引用：5難度：0.8
解析
2．已知函數
f
（
x
）
=
x
在點x=x₀處的切線的傾斜角是
π
4
，則x₀的值為（　　）
A．
1
4
B．
1
2
C．
2
2
D．1
組卷：335引用：5難度：0.8
解析
3．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
的離心率
e
=
4
3
，且其右焦點為F（4，0），則雙曲線C的方程為（　　）
A．
x
2
4
-
y
2
3
=
1
B．
x
2
3
-
y
2
4
=
1
C．
x
2
9
-
y
2
7
=
1
D．
x
2
7
-
y
2
9
=
1
組卷：63引用：5難度：0.7
解析
4．曲線y=x²和曲線y²=x圍成的圖形面積是（　　）
A．
1
3
B．
2
3
C．1 D．
4
3
組卷：208引用：24難度：0.9
解析
5．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點分別為F₁，F₂，過C的左焦點作一條直線與橢圓相交于A，B兩點，若
B
F
1
=
F
1
H
=
HA
且
H
F
2
?
AB
=
0
，則C的離心率為（　　）
A．
1
3
B．
2
3
C．
1
2
D．
3
2
組卷：133引用：2難度：0.5
解析
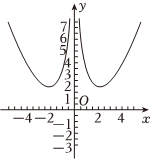6．已知函數y=f（x）的大致圖象如圖所示，則f（x）的解析式可能為（　　）
A．
f
（
x
）
=
e
x
+
e
-
x
x
2
B．
f
（
x
）
=
e
x
-
e
-
x
x
2
C．
f
（
x
）
=
x
2
+
1
x
2
D．
f
（
x
）
=
x
+
1
x
3
組卷：62引用：3難度：0.7
解析
7．若x,y滿足約束條件
2
x
-
y
≥
0

，

x
+
2
y
-
5
≥
0

，

3
x
+
y
-
10
≤
0

，

則z=x²+y²的最大值是（　　）
A．5 B．10 C．
2
5
D．20
組卷：54引用：5難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共6小題，第17題10分，其余每題12分，共70分）

21．已知復數z=a+bi（a,b∈R）．
（1）若復數z在復平面內對應的點位于實軸上方（不包括實軸），求a,b滿足的條件；
（2）若（a+2）-2ai=-3b+（b-1）i,求a,b的值．
組卷：25引用：2難度：0.8
解析

22．某地經過多年的環境治理，已將荒山改造成了綠水青山．為估計一林區某種樹木的材積量，隨機選取了10棵這種樹木，測量每棵樹的根部橫截面積（單位：m²）和材積量（單位：m³），得到如下數據：

樣本號i 1 2 3 4 5 6 7 8 9 10 總和

根部橫截面積x_i 0.04 0.06 0.04 0.08 0.08 0.05 0.05 0.07 0.07 0.06 0.6

材積量y_i 0.25 0.40 0.22 0.54 0.51 0.34 0.36 0.46 0.42 0.40 3.9

由散點圖知根部橫截面積與材積量線性相關，并計算得
10
∑
i
=
1
x
2
i
=
0
.
038
，
10
∑
i
=
1
x
i
y
i
=
0
.
2474
．
（1）估計該林區這種樹木平均一棵的根部橫截面積與平均一棵的材積量；
（2）求該林區這種樹木的根部橫截面積與材積量的回歸直線方程；
（3）現測量了該林區2500棵這種樹木的根部橫截面積，并得到這些樹木的根部橫截面積總和為
2500
∑
i
=
1
x
i
=
153
m
2
．利用（2）中所求的回歸直線方程，估計這些樹木的總材積量．
附：回歸直線方程的斜率
?
b
=
n
∑
i
=
1
x
i
y
i
-
n
x
y
n
∑
i
=
1
x
2
i
-
n
x
2
，截距
?
a
=
y
-
?
b
x
．

組卷：19引用：2難度：0.6

解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A． f （ x ） = e x + e - x x 2	B． f （ x ） = e x - e - x x 2
C． f （ x ） = x 2 + 1 x 2	D． f （ x ） = x + 1 x 3

樣本號i	1	2	3	4	5	6	7	8	9	10	總和
根部橫截面積x_i	0.04	0.06	0.04	0.08	0.08	0.05	0.05	0.07	0.07	0.06	0.6
材積量y_i	0.25	0.40	0.22	0.54	0.51	0.34	0.36	0.46	0.42	0.40	3.9

2022-2023學年山西省大同市陽高四中高二（下）期末數學試卷

一、選擇題（本大題共12道小題，每小題5分，共計60分。在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．i為虛數單位，則i2i4+i=（ ）

2．已知函數f（x）=x在點x=x0處的切線的傾斜角是π4，則x0的值為（ ）

3．已知雙曲線C：x2a2-y2b2=1的離心率e=43，且其右焦點為F（4，0），則雙曲線C的方程為（ ）

4．曲線y=x2和曲線y2=x圍成的圖形面積是（ ）

5．已知橢圓C：x2a2+y2b2=1（a＞b＞0）的左、右焦點分別為F1，F2，過C的左焦點作一條直線與橢圓相交于A，B兩點，若BF1=F1H=HA且HF2?AB=0，則C的離心率為（ ）

6．已知函數y=f（x）的大致圖象如圖所示，則f（x）的解析式可能為（ ）

7．若x,y滿足約束條件2x-y ≥ 0 ， x+2y-5 ≥ 0 ， 3x+y-10 ≤ 0 ， 則z=x2+y2的最大值是（ ）

三、解答題（本大題共6小題，第17題10分，其余每題12分，共70分）

21．已知復數z=a+bi（a,b∈R）．（1）若復數z在復平面內對應的點位于實軸上方（不包括實軸），求a,b滿足的條件；（2）若（a+2）-2ai=-3b+（b-1）i,求a,b的值．

1．i為虛數單位，則
i
2
i
4
+
i
=（　　）

2．已知函數
f
（
x
）
=
x
在點x=x₀處的切線的傾斜角是
π
4
，則x₀的值為（　　）

3．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
的離心率
e
=
4
3
，且其右焦點為F（4，0），則雙曲線C的方程為（　　）

4．曲線y=x²和曲線y²=x圍成的圖形面積是（　　）

5．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點分別為F₁，F₂，過C的左焦點作一條直線與橢圓相交于A，B兩點，若
B
F
1
=
F
1
H
=
HA
且
H
F
2
?
AB
=
0
，則C的離心率為（　　）

6．已知函數y=f（x）的大致圖象如圖所示，則f（x）的解析式可能為（　　）

7．若x,y滿足約束條件
2
x
-
y
≥
0

，

x
+
2
y
-
5
≥
0

，

3
x
+
y
-
10
≤
0

，

則z=x²+y²的最大值是（　　）

21．已知復數z=a+bi（a,b∈R）．
（1）若復數z在復平面內對應的點位于實軸上方（不包括實軸），求a,b滿足的條件；
（2）若（a+2）-2ai=-3b+（b-1）i,求a,b的值．