2023年江蘇省南通市基地大聯考高考數學診斷試卷（3月份）

一、選擇題．本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．設集合A={x|log₃x＜1，x∈Z}，則滿足A∪B={1，2，3，4}的集合B的個數為（　　）

  A．2

  B．3

  C．4

  D．8
  組卷：92引用：4難度：0.8

  解析

• 2．在等差數列{a_n}中，若a₈=6，a₁₁=0，則a₂=（　　）

  A．16

  B．18

  C．20

  D．22
  組卷：421引用：5難度：0.8

  解析

• 3．命題“?x∈[1，2]，x²-a≤0”是真命題的一個必要不充分條件是（　　）

  A．a＞4

  B．a≥4

  C．a＜1

  D．a≥1
  組卷：215引用：4難度：0.7

  解析

• 4．任何一個復數z=a+bi（a,b∈R）都可以表示成z=r（cosθ+isinθ）（r≥0，θ∈R）的形式，通常稱之為復數的三角形式．法國數學家棣莫弗發現：[r（cosθ+isinθ）]ⁿ=rⁿ（cosnθ+isinnθ）（n∈Z），我們稱這個結論為棣莫弗定理．則

  （

  1

  -

  3

  i

  ）

  2022

  =（　　）

  A．1

  B．22022

  C．-22022

  D．i
  組卷：153引用：3難度：0.8

  解析

• 5．已知函數f（x）同時滿足下列條件：①定義域為R；②f（1）=1；③f（x+1）為偶函數；④f（2-x）=-f（2+x），則f（-2）+f（7）=（　　）

  A．-1

  B．0

  C．1

  D．2
  組卷：163引用：5難度：0.6

  解析

• 6．在△ABC中，已知A=60°，BC=2，D為BC的中點，則線段AD長度的最大值為（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：442引用：11難度：0.6

  解析

• 7．如圖1所示，拋物面天線是指由拋物面（拋物線繞其對稱軸旋轉形成的曲面）反射器和位于焦點上的照射器（饋源，通常采用喇叭天線）組成的單反射面型天線，廣泛應用于微波和衛星通訊等領域，具有結構簡單、方向性強、工作頻帶寬等特點．圖2是圖1的軸截面，A，B兩點關于拋物線的對稱軸對稱，F是拋物線的焦點，∠AFB是饋源的方向角，記為θ，焦點F到頂點的距離f與口徑d的比值

  f

  d

  稱為拋物面天線的焦徑比，它直接影響天線的效率與信噪比等．如果某拋物面天線饋源的方向角θ滿足，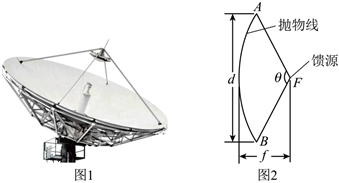

  tanθ

  =

  -

  4

  5

  ，則其焦徑比為（　　）
  

  A． 10 4

  B． 10 8

  C． 5 4

  D． 5 8
  組卷：116引用：3難度：0.5

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知A，B是橢圓

  C

  ：

  x

  2

  4

  +

  y

  2

  3

  =

  1

  上關于坐標原點O對稱的兩點，點D（4，0），連結DA并延長交C于點M，連結DB交C于點N．
  （1）若A為線段DM的中點，求點A的坐標；
  （2）設△DMN，△DAB的面積分別為S₁，S₂，若

  S

  1

  S

  2

  =

  3

  7

  ，求線段OA的長．
  組卷：180引用：3難度：0.3

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  m

  e

  x

  -

  3

  2

  x

  2

  -

  2

  x

  ．
  （1）當m≥3時，證明：f（x）在區間（-∞，+∞）上單調遞增；
  （2）若函數g（x）=f（x）-cosx存在兩個不同的極值點，求實數m的取值范圍．
  組卷：116引用：3難度：0.4

  解析