2012年第十屆“創新杯”全國數學邀請賽試卷（六年級）（1）

一、選擇題（每題8分，共40分）

• 1．下列圖形，第10個圖中△比〇多（　　）個
  

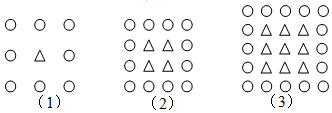
  A．44

  B．60

  C．56

  D．45
  組卷：109引用：2難度：0.9

  解析

• 2．某校學生到郊外植樹，已知老師是學生人數的

  1

  3

  ．若每位男生種13棵樹，女生每人種10棵樹，每個老師種15棵樹，他們共種了204棵樹，那么老師有（　　）人．

  A．6

  B．7

  C．5

  D．4
  組卷：143引用：2難度：0.7

  解析

• 3．如圖，每個小方格面積為1，那么△ABC面積為（　　）
  

  A．10

  B．11

  C．12

  D．11.5
  組卷：76引用：5難度：0.9

  解析

• 4．某工程，可由若干臺機器在規定時間內完成．如果增加兩臺機器，則節省了

  1

  8

  的時間，如果減少兩臺機器，就要推遲

  2

  3

  小時做完．那么一臺機器完成這個工程需要（　　）小時．

  A．56

  B．60

  C．58

  D．42
  組卷：128引用：3難度：0.7

  解析

二、填空題（每題6分，共60分）

• 5．已知

  AA

  ×

  AB

  ×

  C

  ×

  ABC

  =

  ABCABC

  ，其中A、B、C、各代表0，1，2，3，4，5，6，7，8，9中的一個數字，要使等式成立，則三位數

  ABC

  =

  ．
  組卷：124引用：2難度：0.7

  解析

三、解答題（第21、22題各15分，23題20分，共50分）

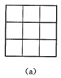• 16．將九個各不相同的正整數填在如圖所示的3×3正方形的格子中（一個格子填一個數），使得每個2×2的正方形中四個數的和都恰好等于100。這九個正整數總和的最小值是多少？
  組卷：13引用：3難度：0.5

  解析

• 17．若k為正整數，則形如：n=1+2+3+…+k=

  1

  2

  k（k+1）的正整數n稱之為三角形數．比如：k=1，2，3，4，5時依次得到的n=1，3，6，10，15都是三角形數．
  （Ⅰ）寫出三位數中最小的三角形數．
  （Ⅱ）如果n是三角形數，證明9n+1也是三角形數．提示：a、b為任意二數，下列計算公式：（a+b）²=a²+2ab+b²
  （Ⅲ）找出一個正整數a和兩個三角形數b（b≠1），n,使得an+b也是三角形數，并給出簡單的證明．（答案不唯一）
  組卷：58引用：5難度：0.3

  解析